5.1: Central Tendency
5.1.1: Mean: The Average
The term central tendency relates to the way in which quantitative data tend to cluster around some value.
Learning Objective
Define the average and distinguish between arithmetic, geometric, and harmonic means.
Key Points
- An average is a measure of the “middle” or “typical” value of a data set.
- The three most common averages are the Pythagorean means – the arithmetic mean, the geometric mean, and the harmonic mean.
- The arithmetic mean is the sum of a collection of numbers divided by the number of numbers in the collection.
- The geometric mean is a type of mean or average which indicates the central tendency, or typical value, of a set of numbers by using the product of their values. It is defined as the
th root (where
is the count of numbers) of the product of the numbers. - The harmonic mean
of the positive real numbers
is defined to be the reciprocal of the arithmetic mean of the reciprocals of
. It is typically appropriate for situations when the average of rates is desired.
Key Terms
- average
-
any measure of central tendency, especially any mean, the median, or the mode
- arithmetic mean
-
the measure of central tendency of a set of values computed by dividing the sum of the values by their number; commonly called the mean or the average
- central tendency
-
a term that relates the way in which quantitative data tend to cluster around some value
Example
- The arithmetic mean, often simply called the mean, of two numbers, such as 2 and 8, is obtained by finding a value
such that
. One may find that
. Switching the order of 2 and 8 to read 8 and 2 does not change the resulting value obtained for A. The mean 5 is not less than the minimum 2 nor greater than the maximum 8. If we increase the number of terms in the list for which we want an average, we get, for example, that the arithmetic mean of 2, 8, and 11 is found by solving for the value of
in the equation
. One finds that
.
The term central tendency relates to the way in which quantitative data tend to cluster around some value. A measure of central tendency is any of a variety of ways of specifying this “central value”. Central tendency is contrasted with statistical dispersion (spread), and together these are the most used properties of distributions. Statistics that measure central tendency can be used in descriptive statistics as a summary statistic for a data set, or as estimators of location parameters of a statistical model.
In the simplest cases, the measure of central tendency is an average of a set of measurements, the word average being variously construed as mean, median, or other measure of location, depending on the context. An average is a measure of the “middle” or “typical” value of a data set. In the most common case, the data set is a list of numbers. The average of a list of numbers is a single number intended to typify the numbers in the list. If all the numbers in the list are the same, then this number should be used. If the numbers are not the same, the average is calculated by combining the numbers from the list in a specific way and computing a single number as being the average of the list.
The term mean has three related meanings:
- The arithmetic mean of a sample,
- The expected value of a random variable, or
- The mean of a probability distribution
The Pythagorean Means
The three most common averages are the Pythagorean means – the arithmetic mean, the geometric mean, and the harmonic mean.

Comparison of Pythagorean Means
Comparison of the arithmetic, geometric and harmonic means of a pair of numbers. The vertical dashed lines are asymptotes for the harmonic means.
The Arithmetic Mean
When we think of means, or averages, we are typically thinking of the arithmetic mean. It is the sum of a collection of numbers divided by the number of numbers in the collection. The collection is often a set of results of an experiment, or a set of results from a survey of a subset of the public. In addition to mathematics and statistics, the arithmetic mean is used frequently in fields such as economics, sociology, and history, and it is used in almost every academic field to some extent. For example, per capita income is the arithmetic average income of a nation’s population.
Suppose we have a data set containing the values
. The arithmetic mean is defined via the expression:
If the data set is a statistical population (i.e., consists of every possible observation and not just a subset of them), then the mean of that population is called the population mean. If the data set is a statistical sample (a subset of the population) we call the statistic resulting from this calculation a sample mean. If it is required to use a single number as an estimate for the values of numbers, then the arithmetic mean does this best. This is because it minimizes the sum of squared deviations from the estimate.
The Geometric Mean
The geometric mean is a type of mean or average which indicates the central tendency, or typical value, of a set of numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean applies only to positive numbers. The geometric mean is defined as the
th root (where
is the count of numbers) of the product of the numbers.
For instance, the geometric mean of two numbers, say 2 and 8, is just the square root of their product; that is
. As another example, the geometric mean of the three numbers 4, 1, and 1/32 is the cube root of their product (1/8), which is 1/2; that is
.
A geometric mean is often used when comparing different items – finding a single “figure of merit” for these items – when each item has multiple properties that have different numeric ranges. The use of a geometric mean “normalizes” the ranges being averaged, so that no range dominates the weighting, and a given percentage change in any of the properties has the same effect on the geometric mean.
For example, the geometric mean can give a meaningful “average” to compare two companies which are each rated at 0 to 5 for their environmental sustainability, and are rated at 0 to 100 for their financial viability. If an arithmetic mean was used instead of a geometric mean, the financial viability is given more weight because its numeric range is larger – so a small percentage change in the financial rating (e.g. going from 80 to 90) makes a much larger difference in the arithmetic mean than a large percentage change in environmental sustainability (e.g. going from 2 to 5).
The Harmonic Mean
The harmonic mean is typically appropriate for situations when the average of rates is desired. It may (compared to the arithmetic mean) mitigate the influence of large outliers and increase the influence of small values.
The harmonic mean
of the positive real numbers
is defined to be the reciprocal of the arithmetic mean of the reciprocals of
. For example, the harmonic mean of 1, 2, and 4 is:
The harmonic mean is the preferable method for averaging multiples, such as the price/earning ratio in Finance, in which price is in the numerator. If these ratios are averaged using an arithmetic mean (a common error), high data points are given greater weights than low data points. The harmonic mean, on the other hand, gives equal weight to each data point.
5.1.2: The Average and the Histogram
The shape of a histogram can assist with identifying other descriptive statistics, such as which measure of central tendency is appropriate to use.
Learning Objective
Demonstrate the effect that the shape of a distribution has on measures of central tendency.
Key Points
- Histograms tend to form shapes, which when measured can describe the distribution of data within a dataset.
- A key feature of the normal distribution is that the mode, median and mean are the same and are together in the center of the curve.
- A key feature of the skewed distribution is that the mean and median have different values and do not all lie at the center of the curve.
- Skewed distributions with two or more modes are known as bi-modal or multimodal, respectively.
Key Terms
- normal distribution
-
A family of continuous probability distributions such that the probability density function is the normal (or Gaussian) function.
- bell curve
-
In mathematics, the bell-shaped curve that is typical of the normal distribution.
- histogram
-
A representation of tabulated frequencies, shown as adjacent rectangles, erected over discrete intervals (bins), with an area equal to the frequency of the observations in the interval.
As discussed, a histogram is a bar graph displaying tabulated frequencies. Histograms tend to form shapes, which when measured can describe the distribution of data within a dataset. The shape of the distribution can assist with identifying other descriptive statistics, such as which measure of central tendency is appropriate to use.
The distribution of data item values may be symmetrical or asymmetrical. Two common examples of symmetry and asymmetry are the “normal distribution” and the “skewed distribution. “
Central Tendency and Normal Distributions
In a symmetrical distribution the two sides of the distribution are a mirror image of each other. A normal distribution is a true symmetric distribution of data item values. When a histogram is constructed on values that are normally distributed, the shape of columns form a symmetrical bell shape. This is why this distribution is also known as a “normal curve” or “bell curve. ” is an example of a normal distribution:
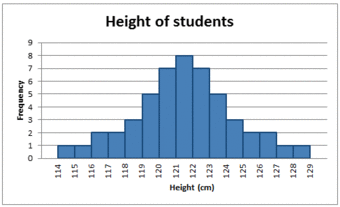
The Normal Distribution
A histogram showing a normal distribution, or bell curve.
If represented as a ‘normal curve’ (or bell curve) the graph would take the following shape (where
is the mean and
is the standard deviation):
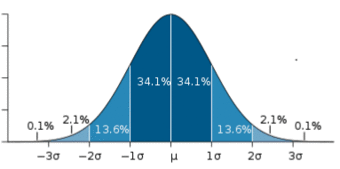
The Bell Curve
The shape of a normally distributed histogram.
A key feature of the normal distribution is that the mode, median and mean are the same and are together in the center of the curve.
Also, there can only be one mode (i.e. there is only one value which is most frequently observed). Moreover, most of the data are clustered around the center, while the more extreme values on either side of the center become less rare as the distance from the center increases (i.e. about 68% of values lie within one standard deviation (
) away from the mean; about 95% of the values lie within two standard deviations; and about 99.7% are within three standard deviations. This is known as the empirical rule or the 3-sigma rule).
Central Tendency and Skewed Distributions
In an asymmetrical distribution the two sides will not be mirror images of each other. Skewness is the tendency for the values to be more frequent around the high or low ends of the
-axis. When a histogram is constructed for skewed data it is possible to identify skewness by looking at the shape of the distribution. For example, a distribution is said to be positively skewed when the tail on the right side of the histogram is longer than the left side. Most of the values tend to cluster toward the left side of the
-axis (i.e, the smaller values) with increasingly fewer values at the right side of the
-axis (i.e. the larger values).
A distribution is said to be negatively skewed when the tail on the left side of the histogram is longer than the right side. Most of the values tend to cluster toward the right side of the
-axis (i.e. the larger values), with increasingly less values on the left side of the
-axis (i.e. the smaller values).
A key feature of the skewed distribution is that the mean and median have different values and do not all lie at the center of the curve.
There can also be more than one mode in a skewed distribution. Distributions with two or more modes are known as bi-modal or multimodal, respectively. The distribution shape of the data in is bi-modal because there are two modes (two values that occur more frequently than any other) for the data item (variable).
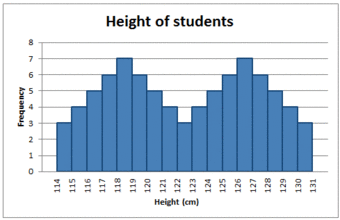
Bi-modal Distribution
Some skewed distributions have two or more modes.
5.1.3: The Root-Mean-Square
The root-mean-square, also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity, or set of numbers.
Learning Objective
Compute the root-mean-square and express its usefulness.
Key Points
- The root-mean-square is especially useful when a data set includes both positive and negative numbers.
- Its name comes from its definition as the square root of the mean of the squares of the values.
- The process of computing the root mean square is to: 1) Square all of the values 2) Compute the average of the squares 3) Take the square root of the average.
- The root-mean-square is always greater than or equal to the average of the unsigned values.
Key Term
- root mean square
-
the square root of the arithmetic mean of the squares
The root-mean-square, also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity, or set of numbers. It can be calculated for a series of discrete values or for a continuously varying function. Its name comes from its definition as the square root of the mean of the squares of the values.
This measure is especially useful when a data set includes both positive and negative numbers. For example, consider the set of numbers
. Computing the average of this set of numbers wouldn’t tell us much because the negative numbers cancel out the positive numbers, resulting in an average of zero. This gives us the “middle value” but not a sense of the average magnitude.
One possible method of assigning an average to this set would be to simply erase all of the negative signs. This would lead us to compute an average of 5.6. However, using the RMS method, we would square every number (making them all positive) and take the square root of the average. Explicitly, the process is to:
- Square all of the values
- Compute the average of the squares
- Take the square root of the average
In our example:
The root-mean-square is always greater than or equal to the average of the unsigned values. Physical scientists often use the term “root-mean-square” as a synonym for standard deviation when referring to the square root of the mean squared deviation of a signal from a given baseline or fit. This is useful for electrical engineers in calculating the “AC only” RMS of an electrical signal. Standard deviation being the root-mean-square of a signal’s variation about the mean, rather than about 0, the DC component is removed (i.e. the RMS of the signal is the same as the standard deviation of the signal if the mean signal is zero).

Mathematical Means
This is a geometrical representation of common mathematical means.
,
are scalars.
is the arithmetic mean of scalars
and
.
is the geometric mean,
is the harmonic mean,
is the quadratic mean (also known as root-mean-square).
5.1.4: Which Average: Mean, Mode, or Median?
Depending on the characteristic distribution of a data set, the mean, median or mode may be the more appropriate metric for understanding.
Learning Objective
Assess various situations and determine whether the mean, median, or mode would be the appropriate measure of central tendency.
Key Points
- In symmetrical, unimodal distributions, such as the normal distribution (the distribution whose density function, when graphed, gives the famous “bell curve”), the mean (if defined), median and mode all coincide.
- If elements in a sample data set increase arithmetically, when placed in some order, then the median and arithmetic mean are equal. For example, consider the data sample
. The mean is 2.5, as is the median. - While the arithmetic mean is often used to report central tendencies, it is not a robust statistic, meaning that it is greatly influenced by outliers (values that are very much larger or smaller than most of the values).
- The median is of central importance in robust statistics, as it is the most resistant statistic, having a breakdown point of 50%: so long as no more than half the data is contaminated, the median will not give an arbitrarily large result.
- Unlike mean and median, the concept of mode also makes sense for “nominal data” (i.e., not consisting of numerical values in the case of mean, or even of ordered values in the case of median).
Key Terms
- Mode
-
the most frequently occurring value in a distribution
- breakdown point
-
the number or proportion of arbitrarily large or small extreme values that must be introduced into a batch or sample to cause the estimator to yield an arbitrarily large result
- median
-
the numerical value separating the higher half of a data sample, a population, or a probability distribution, from the lower half
Example
- The mode is the value that appears most often in a set of data. For example, the mode of the sample
is 6. The median of a finite list of numbers can be found by arranging all the observations from lowest value to highest value and picking the middle one (e.g., the median of
is 5).
The Mode
The mode is the value that appears most often in a set of data. For example, the mode of the sample
is 6. Like the statistical mean and median, the mode is a way of expressing, in a single number, important information about a random variable or a population.
The mode is not necessarily unique, since the same maximum frequency may be attained at different values. Given the list of data
the mode is not unique – the dataset may be said to be bimodal, while a set with more than two modes may be described as multimodal. The most extreme case occurs in uniform distributions, where all values occur equally frequently.
For a sample from a continuous distribution, the concept is unusable in its raw form. No two values will be exactly the same, so each value will occur precisely once. In order to estimate the mode, the usual practice is to discretize the data by assigning frequency values to intervals of equal distance, as with making a histogram, effectively replacing the values with the midpoints of the intervals they are assigned to. The mode is then the value where the histogram reaches its peak.
The Median
The median is the numerical value separating the higher half of a data sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to highest value and picking the middle one (e.g., the median of
is 5). If there is an even number of observations, then there is no single middle value. In this case, the median is usually defined to be the mean of the two middle values.
The median can be used as a measure of location when a distribution is skewed, when end-values are not known, or when one requires reduced importance to be attached to outliers (e.g., because there may be measurement errors).
Which to Use?
In symmetrical, unimodal distributions, such as the normal distribution (the distribution whose density function, when graphed, gives the famous “bell curve”), the mean (if defined), median and mode all coincide. For samples, if it is known that they are drawn from a symmetric distribution, the sample mean can be used as an estimate of the population mode.
If elements in a sample data set increase arithmetically, when placed in some order, then the median and arithmetic mean are equal. For example, consider the data sample
. The mean is 2.5, as is the median. However, when we consider a sample that cannot be arranged so as to increase arithmetically, such as
, the median and arithmetic mean can differ significantly. In this case, the arithmetic mean is 6.2 and the median is 4. In general the average value can vary significantly from most values in the sample, and can be larger or smaller than most of them.
While the arithmetic mean is often used to report central tendencies, it is not a robust statistic, meaning that it is greatly influenced by outliers (values that are very much larger or smaller than most of the values). Notably, for skewed distributions, such as the distribution of income for which a few people’s incomes are substantially greater than most people’s, the arithmetic mean may not be consistent with one’s notion of “middle,” and robust statistics such as the median may be a better description of central tendency.
The median is of central importance in robust statistics, as it is the most resistant statistic, having a breakdown point of 50%: so long as no more than half the data is contaminated, the median will not give an arbitrarily large result. Robust statistics are statistics with good performance for data drawn from a wide range of probability distributions, especially for distributions that are not normally distributed. One motivation is to produce statistical methods that are not unduly affected by outliers. Another motivation is to provide methods with good performance when there are small departures from parametric distributions.
Unlike median, the concept of mean makes sense for any random variable assuming values from a vector space. For example, a distribution of points in the plane will typically have a mean and a mode, but the concept of median does not apply.
Unlike mean and median, the concept of mode also makes sense for “nominal data” (i.e., not consisting of numerical values in the case of mean, or even of ordered values in the case of median). For example, taking a sample of Korean family names, one might find that “Kim” occurs more often than any other name. Then “Kim” would be the mode of the sample. In any voting system where a plurality determines victory, a single modal value determines the victor, while a multi-modal outcome would require some tie-breaking procedure to take place.
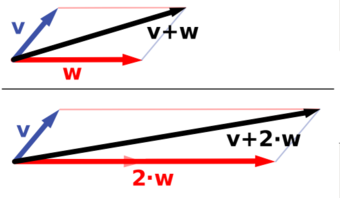
Vector Space
Vector addition and scalar multiplication: a vector
(blue) is added to another vector
(red, upper illustration). Below,
is stretched by a factor of 2, yielding the sum
.

Comparison of the Mean, Mode & Median
Comparison of mean, median and mode of two log-normal distributions with different skewness.
5.1.5: Averages of Qualitative and Ranked Data
The central tendency for qualitative data can be described via the median or the mode, but not the mean.
Learning Objective
Categorize levels of measurement and identify the appropriate measures of central tendency.
Key Points
- Qualitative data can be defined as either nominal or ordinal.
- The nominal scale differentiates between items or subjects based only on their names and/or categories and other qualitative classifications they belong to.
- The mode is allowed as the measure of central tendency for nominal data.
- The ordinal scale allows for rank order by which data can be sorted, but still does not allow for relative degree of difference between them. The median and the mode are allowed as the measure of central tendency; however, the mean as the measure of central tendency is not allowed.
- The median and the mode are allowed as the measure of central tendency for ordinal data; however, the mean as the measure of central tendency is not allowed.
Key Terms
- quantitative
-
of a measurement based on some quantity or number rather than on some quality
- qualitative
-
of descriptions or distinctions based on some quality rather than on some quantity
- dichotomous
-
dividing or branching into two pieces
Levels of Measurement
In order to address the process for finding averages of qualitative data, we must first introduce the concept of levels of measurement. In statistics, levels of measurement, or scales of measure, are types of data that arise in the theory of scale types developed by the psychologist Stanley Smith Stevens. Stevens proposed his typology in a 1946 Science article entitled “On the Theory of Scales of Measurement. ” In that article, Stevens claimed that all measurement in science was conducted using four different types of scales that he called “nominal”, “ordinal”, “interval” and “ratio”, unifying both qualitative (which are described by his “nominal” type) and quantitative (to a different degree, all the rest of his scales).
Nominal Scale
The nominal scale differentiates between items or subjects based only on their names and/or categories and other qualitative classifications they belong to. Examples include gender, nationality, ethnicity, language, genre, style, biological species, visual pattern, and form.
The mode, i.e. the most common item, is allowed as the measure of central tendency for the nominal type. On the other hand, the median, i.e. the middle-ranked item, makes no sense for the nominal type of data since ranking is not allowed for the nominal type.
Ordinal Scale
The ordinal scale allows for rank order (1st, 2nd, 3rd, et cetera) by which data can be sorted, but still does not allow for relative degree of difference between them. Examples include, on one hand, dichotomous data with dichotomous (or dichotomized) values such as “sick” versus “healthy” when measuring health, “guilty” versus “innocent” when making judgments in courts, or “wrong/false” versus “right/true” when measuring truth value. On the other hand, non-dichotomous data consisting of a spectrum of values is also included, such as “completely agree,” “mostly agree,” “mostly disagree,” and “completely disagree” when measuring opinion .
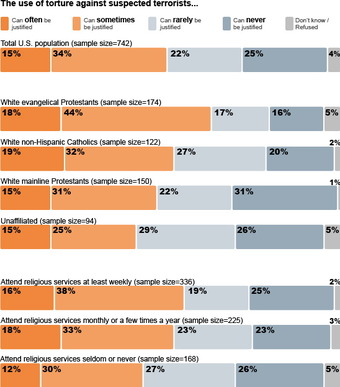
Ordinal Scale Surveys
An opinion survey on religiosity and torture. An opinion survey is an example of a non-dichotomous data set on the ordinal scale for which the central tendency can be described by the median or the mode.
The median, i.e. middle-ranked, item is allowed as the measure of central tendency; however, the mean (or average) as the measure of central tendency is not allowed. The mode is also allowed.
In 1946, Stevens observed that psychological measurement, such as measurement of opinions, usually operates on ordinal scales; thus means and standard deviations have no validity, but they can be used to get ideas for how to improve operationalization of variables used in questionnaires.
5.2: Measures of Relative Standing
5.2.1: Measures of Relative Standing
Measures of relative standing can be used to compare values from different data sets, or to compare values within the same data set.
Learning Objective
Outline how percentiles and quartiles measure relative standing within a data set.
Key Points
- The common measures of relative standing or location are quartiles and percentiles.
- A percentile is a measure used in statistics indicating the value below which a given percentage of observations in a group of observations fall.
- The 25th percentile is also known as the first quartile (Q1), the 50th percentile as the median or second quartile (Q2), and the 75th percentile as the third quartile (Q3).
- To calculate quartiles and percentiles, the data must be ordered from smallest to largest.
- For very large populations following a normal distribution, percentiles may often be represented by reference to a normal curve plot.
- Percentiles represent the area under the normal curve, increasing from left to right.
Key Terms
- percentile
-
any of the ninety-nine points that divide an ordered distribution into one hundred parts, each containing one per cent of the population
- quartile
-
any of the three points that divide an ordered distribution into four parts, each containing a quarter of the population
Example
- a. For runners in a race, a low time means a faster run. The winners in a race have the shortest running times. Is it more desirable to have a finish time with a high or a low percentile when running a race? b. The 20th percentile of run times in a particular race is 5.2 minutes. Write a sentence interpreting the 20th percentile in the context of the situation. c. A bicyclist in the 90th percentile of a bicycle race between two towns completed the race in 1 hour and 12 minutes. Is he among the fastest or slowest cyclists in the race? Write a sentence interpreting the 90th percentile in the context of the situation. SOLUTION a. For runners in a race it is more desirable to have a low percentile for finish time. A low percentile means a short time, which is faster. b. INTERPRETATION: 20% of runners finished the race in 5.2 minutes or less. 80% of runners finished the race in 5.2 minutes or longer. c. He is among the slowest cyclists (90% of cyclists were faster than him. ) INTERPRETATION: 90% of cyclists had a finish time of 1 hour, 12 minutes or less.Only 10% of cyclists had a finish time of 1 hour, 12 minutes or longer.
Measures of relative standing, in the statistical sense, can be defined as measures that can be used to compare values from different data sets, or to compare values within the same data set.
Quartiles and Percentiles
The common measures of relative standing or location are quartiles and percentiles. A percentile is a measure used in statistics indicating the value below which a given percentage of observations in a group of observations fall. For example, the 20th percentile is the value (or score) below which 20 percent of the observations may be found. The term percentile and the related term, percentile rank, are often used in the reporting of scores from norm-referenced tests. For example, if a score is in the 86th percentile, it is higher than 86% of the other scores. The 25th percentile is also known as the first quartile (Q1), the 50th percentile as the median or second quartile (Q2), and the 75th percentile as the third quartile (Q3).
To calculate quartiles and percentiles, the data must be ordered from smallest to largest. Recall that quartiles divide ordered data into quarters. Percentiles divide ordered data into hundredths. To score in the 90th percentile of an exam does not mean, necessarily, that you received 90% on a test. It means that 90% of test scores are the same or less than your score and 10% of the test scores are the same or greater than your test score.
Percentiles are useful for comparing values. For this reason, universities and colleges use percentiles extensively. Percentiles are mostly used with very large populations. Therefore, if you were to say that 90% of the test scores are less (and not the same or less) than your score, it would be acceptable because removing one particular data value is not significant.
For very large populations following a normal distribution, percentiles may often be represented by reference to a normal curve plot. The normal distribution is plotted along an axis scaled to standard deviations, or sigma units. Percentiles represent the area under the normal curve, increasing from left to right. Each standard deviation represents a fixed percentile. Thus, rounding to two decimal places,
is the 0.13th percentile,
the 2.28th percentile,
the 15.87th percentile, 0 the 50th percentile (both the mean and median of the distribution),
the 84.13th percentile,
the 97.72nd percentile, and
the 99.87th percentile. This is known as the 68–95–99.7 rule or the three-sigma rule.

Percentile Diagram
Representation of the 68–95–99.7 rule. The dark blue zone represents observations within one standard deviation (
) to either side of the mean (
), which accounts for about 68.2% of the population. Two standard deviations from the mean (dark and medium blue) account for about 95.4%, and three standard deviations (dark, medium, and light blue) for about 99.7%.
Note that in theory the 0th percentile falls at negative infinity and the 100th percentile at positive infinity; although, in many practical applications, such as test results, natural lower and/or upper limits are enforced.
Interpreting Percentiles, Quartiles, and Median
A percentile indicates the relative standing of a data value when data are sorted into numerical order, from smallest to largest.
% of data values are less than or equal to the th percentile. For example, 15% of data values are less than or equal to the 15th percentile. Low percentiles always correspond to lower data values. High percentiles always correspond to higher data values.
A percentile may or may not correspond to a value judgment about whether it is “good” or “bad”. The interpretation of whether a certain percentile is good or bad depends on the context of the situation to which the data applies. In some situations, a low percentile would be considered “good’; in other contexts a high percentile might be considered “good”. In many situations, there is no value judgment that applies.
Understanding how to properly interpret percentiles is important not only when describing data, but is also important when calculating probabilities.
Guideline:
When writing the interpretation of a percentile in the context of the given data, the sentence should contain the following information:
- information about the context of the situation being considered,
- the data value (value of the variable) that represents the percentile,
- the percent of individuals or items with data values below the percentile.
- Additionally, you may also choose to state the percent of individuals or items with data values above the percentile.
5.2.2: Median
The median is the middle value in distribution when the values are arranged in ascending or descending order.
Learning Objective
Identify the median in a data set and distinguish it’s properties from other measures of central tendency.
Key Points
- The median divides the distribution in half (there are 50% of observations on either side of the median value). In a distribution with an odd number of observations, the median value is the middle value.
- When the distribution has an even number of observations, the median value is the mean of the two middle values.
- The median is less affected by outliers and skewed data than the mean, and is usually the preferred measure of central tendency when the distribution is not symmetrical.
- he median cannot be identified for categorical nominal data, as it cannot be logically ordered.
Key Terms
- outlier
-
a value in a statistical sample which does not fit a pattern that describes most other data points; specifically, a value that lies 1.5 IQR beyond the upper or lower quartile
- median
-
the numerical value separating the higher half of a data sample, a population, or a probability distribution, from the lower half
A measure of central tendency (also referred to as measures of center or central location) is a summary measure that attempts to describe a whole set of data with a single value that represents the middle or center of its distribution. There are three main measures of central tendency: the mode, the median and the mean . Each of these measures describes a different indication of the typical or central value in the distribution.

Central tendency
Comparison of mean, median and mode of two log-normal distributions with different skewness.
The median is the middle value in distribution when the values are arranged in ascending or descending order. The median divides the distribution in half (there are 50% of observations on either side of the median value). In a distribution with an odd number of observations, the median value is the middle value.
Looking at the retirement age distribution (which has 11 observations), the median is the middle value, which is 57 years:
54, 54, 54, 55, 56, 57, 57, 58, 58, 60, 60
When the distribution has an even number of observations, the median value is the mean of the two middle values. In the following distribution, the two middle values are 56 and 57, therefore the median equals 56.5 years:
52, 54, 54, 54, 55, 56, 57, 57, 58, 58, 60, 60
The median is less affected by outliers and skewed data than the mean, and is usually the preferred measure of central tendency when the distribution is not symmetrical. The median cannot be identified for categorical nominal data, as it cannot be logically ordered.
5.2.3: Mode
The mode is the most commonly occurring value in a distribution.
Learning Objective
Define the mode and explain its limitations.
Key Points
- There are some limitations to using the mode. In some distributions, the mode may not reflect the center of the distribution very well.
- It is possible for there to be more than one mode for the same distribution of data, (eg bi-modal). The presence of more than one mode can limit the ability of the mode in describing the center or typical value of the distribution because a single value to describe the center cannot be identified.
- In some cases, particularly where the data are continuous, the distribution may have no mode at all (i.e. if all values are different). In cases such as these, it may be better to consider using the median or mean, or group the data in to appropriate intervals, and find the modal class.
Key Term
- skewness
-
A measure of the asymmetry of the probability distribution of a real-valued random variable; is the third standardized moment, defined as where is the third moment about the mean and is the standard deviation.
A measure of central tendency (also referred to as measures of center or central location) is a summary measure that attempts to describe a whole set of data with a single value that represents the middle or center of its distribution. There are three main measures of central tendency: the mode, the median and the mean . Each of these measures describes a different indication of the typical skewness in the distribution.

Mean, Media and Mode
Comparison of mean, median and mode of two log-normal distributions with different skewness.
The mode is the most commonly occurring value in a distribution. Consider this dataset showing the retirement age of 11 people, in whole years:
54, 54, 54, 55, 56, 57, 57, 58, 58, 60, 60
The most commonly occurring value is 54, therefore the mode of this distribution is 54 years. The mode has an advantage over the median and the mean as it can be found for both numerical and categorical (non-numerical) data.
There are some limitations to using the mode. In some distributions, the mode may not reflect the center of the distribution very well. When the distribution of retirement age is ordered from lowest to highest value, it is easy to see that the center of the distribution is 57 years, but the mode is lower, at 54 years. It is also possible for there to be more than one mode for the same distribution of data, (bi-modal, or multi-modal). The presence of more than one mode can limit the ability of the mode in describing the center or typical value of the distribution because a single value to describe the center cannot be identified. In some cases, particularly where the data are continuous, the distribution may have no mode at all (i.e. if all values are different). In cases such as these, it may be better to consider using the median or mean, or group the data in to appropriate intervals, and find the modal class.
5.3: The Law of Averages
5.3.1: What Does the Law of Averages Say?
The law of averages is a lay term used to express a belief that outcomes of a random event will “even out” within a small sample.
Learning Objective
Evaluate the law of averages and distinguish it from the law of large numbers.
Key Points
- The law of averages typically assumes that unnatural short-term “balance” must occur. This can also be known as “Gambler’s Fallacy” and is not a real mathematical principle.
- Some people mix up the law of averages with the law of large numbers, which is a real theorem that states that the average of the results obtained from a large number of trials should be close to the expected value, and will tend to become closer as more trials are performed.
- The law of large numbers is important because it “guarantees” stable long-term results for the averages of random events. It does not guarantee what will happen with a small number of events.
Key Term
- expected value
-
of a discrete random variable, the sum of the probability of each possible outcome of the experiment multiplied by the value itself
The Law of Averages
The law of averages is a lay term used to express a belief that outcomes of a random event will “even out” within a small sample. As invoked in everyday life, the “law” usually reflects bad statistics or wishful thinking rather than any mathematical principle. While there is a real theorem that a random variable will reflect its underlying probability over a very large sample (the law of large numbers), the law of averages typically assumes that unnatural short-term “balance” must occur.
The law of averages is sometimes known as “Gambler’s Fallacy. ” It evokes the idea that an event is “due” to happen. For example, “The roulette wheel has landed on red in three consecutive spins. The law of averages says it’s due to land on black! ” Of course, the wheel has no memory and its probabilities do not change according to past results. So even if the wheel has landed on red in ten consecutive spins, the probability that the next spin will be black is still 48.6% (assuming a fair European wheel with only one green zero: it would be exactly 50% if there were no green zero and the wheel were fair, and 47.4% for a fair American wheel with one green “0” and one green “00”). (In fact, if the wheel has landed on red in ten consecutive spins, that is strong evidence that the wheel is not fair – that it is biased toward red. Thus, the wise course on the eleventh spin would be to bet on red, not on black: exactly the opposite of the layman’s analysis.) Similarly, there is no statistical basis for the belief that lottery numbers which haven’t appeared recently are due to appear soon.
The Law of Large Numbers
Some people interchange the law of averages with the law of large numbers, but they are different. The law of averages is not a mathematical principle, whereas the law of large numbers is. In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value, and will tend to become closer as more trials are performed.
The law of large numbers is important because it “guarantees” stable long-term results for the averages of random events. For example, while a casino may lose money in a single spin of the roulette wheel, its earnings will tend towards a predictable percentage over a large number of spins. Any winning streak by a player will eventually be overcome by the parameters of the game. It is important to remember that the law of large numbers only applies (as the name indicates) when a large number of observations are considered. There is no principle that a small number of observations will coincide with the expected value or that a streak of one value will immediately be “balanced” by the others.
Another good example comes from the expected value of rolling a six-sided die. A single roll produces one of the numbers 1, 2, 3, 4, 5, or 6, each with an equal probability (
) of occurring. The expected value of a roll is 3.5, which comes from the following equation:
According to the law of large numbers, if a large number of six-sided dice are rolled, the average of their values (sometimes called the sample mean) is likely to be close to 3.5, with the accuracy increasing as more dice are rolled . However, in a small number of rolls, just because ten 6’s are rolled in a row, it doesn’t mean a 1 is more likely the next roll. Each individual outcome still has a probability of
.

The Law of Large Numbers
This shows a graph illustrating the law of large numbers using a particular run of rolls of a single die. As the number of rolls in this run increases, the average of the values of all the results approaches 3.5. While different runs would show a different shape over a small number of throws (at the left), over a large number of rolls (to the right) they would be extremely similar.
5.3.2: Chance Processes
A stochastic process is a collection of random variables that is often used to represent the evolution of some random value over time.
Learning Objective
Summarize the stochastic process and state its relationship to random walks.
Key Points
- One approach to stochastic processes treats them as functions of one or several deterministic arguments (inputs, in most cases regarded as time) whose values (outputs) are random variables.
- Random variables are non-deterministic (single) quantities which have certain probability distributions.
- Although the random values of a stochastic process at different times may be independent random variables, in most commonly considered situations they exhibit complicated statistical correlations.
- The law of a stochastic process is the measure that the process induces on the collection of functions from the index set into the state space.
- A random walk is a mathematical formalization of a path that consists of a succession of random steps.
Key Terms
- random variable
-
a quantity whose value is random and to which a probability distribution is assigned, such as the possible outcome of a roll of a die
- random walk
-
a stochastic path consisting of a series of sequential movements, the direction (and sometime length) of which is chosen at random
- stochastic
-
random; randomly determined
Example
- Familiar examples of processes modeled as stochastic time series include stock market and exchange rate fluctuations; signals such as speech, audio and video; medical data such as a patient’s EKG, EEG, blood pressure or temperature; and random movement such as Brownian motion or random walks.
Chance = Stochastic
In probability theory, a stochastic process–sometimes called a random process– is a collection of random variables that is often used to represent the evolution of some random value, or system, over time. It is the probabilistic counterpart to a deterministic process (or deterministic system). Instead of describing a process which can only evolve in one way (as in the case, for example, of solutions of an ordinary differential equation), in a stochastic or random process there is some indeterminacy. Even if the initial condition (or starting point) is known, there are several (often infinitely many) directions in which the process may evolve.
In the simple case of discrete time, a stochastic process amounts to a sequence of random variables known as a time series–for example, a Markov chain. Another basic type of a stochastic process is a random field, whose domain is a region of space. In other words, a stochastic process is a random function whose arguments are drawn from a range of continuously changing values.
One approach to stochastic processes treats them as functions of one or several deterministic arguments (inputs, in most cases regarded as time) whose values (outputs) are random variables. Random variables are non-deterministic (single) quantities which have certain probability distributions. Random variables corresponding to various times (or points, in the case of random fields) may be completely different. Although the random values of a stochastic process at different times may be independent random variables, in most commonly considered situations they exhibit complicated statistical correlations.
Familiar examples of processes modeled as stochastic time series include stock market and exchange rate fluctuations; signals such as speech, audio, and video; medical data such as a patient’s EKG, EEG, blood pressure, or temperature; and random movement such as Brownian motion or random walks.
Law of a Stochastic Process
The law of a stochastic process is the measure that the process induces on the collection of functions from the index set into the state space. The law encodes a lot of information about the process. In the case of a random walk, for example, the law is the probability distribution of the possible trajectories of the walk.
A random walk is a mathematical formalization of a path that consists of a succession of random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock, and the financial status of a gambler can all be modeled as random walks, although they may not be truly random in reality. Random walks explain the observed behaviors of processes in such fields as ecology, economics, psychology, computer science, physics, chemistry, biology and, of course, statistics. Thus, the random walk serves as a fundamental model for recorded stochastic activity.

Random Walk
Example of eight random walks in one dimension starting at 0. The plot shows the current position on the line (vertical axis) versus the time steps (horizontal axis).
5.3.3: The Sum of Draws
The sum of draws is the process of drawing randomly, with replacement, from a set of data and adding up the results.
Learning Objective
Describe how chance variation affects sums of draws.
Key Points
- By drawing from a set of data with replacement, we are able to draw over and over again under the same conditions.
- The sum of draws is subject to a force known as chance variation.
- The sum of draws can be illustrated in practice through a game of Monopoly. A player rolls a pair of dice, adds the two numbers on the die, and moves his or her piece that many squares.
Key Term
- chance variation
-
the presence of chance in determining the variation in experimental results
The sum of draws can be illustrated by the following process. Imagine there is a box of tickets, each having a number 1, 2, 3, 4, 5, or 6 written on it.
The sum of draws can be represented by a process in which tickets are drawn at random from the box, with the ticket being replaced to the box after each draw. Then, the numbers on these tickets are added up. By replacing the tickets after each draw, you are able to draw over and over under the same conditions.
Say you draw twice from the box at random with replacement. To find the sum of draws, you simply add the first number you drew to the second number you drew. For instance, if first you draw a 4 and second you draw a 6, your sum of draws would be
. You could also first draw a 4 and then draw 4 again. In this case your sum of draws would be
. Your sum of draws is, therefore, subject to a force known as chance variation.
This example can be seen in practical terms when imagining a turn of Monopoly. A player rolls a pair of dice, adds the two numbers on the die, and moves his or her piece that many squares. Rolling a die is the same as drawing a ticket from a box containing six options.

Sum of Draws In Practice
Rolling a die is the same as drawing a ticket from a box containing six options.
To better see the affects of chance variation, let us take 25 draws from the box. These draws result in the following values:
3 2 4 6 3 3 5 4 4 1 3 6 4 1 3 4 1 5 5 5 2 2 2 5 6
The sum of these 25 draws is 89. Obviously this sum would have been different had the draws been different.
5.3.4: Making a Box Model
A box plot (also called a box-and-whisker diagram) is a simple visual representation of key features of a univariate sample.
Learning Objective
Produce a box plot that is representative of a data set.
Key Points
- Our ultimate goal in statistics is not to summarize the data, it is to fully understand their complex relationships.
- A well designed statistical graphic helps us explore, and perhaps understand, these relationships.
- A common extension of the box model is the ‘box-and-whisker’ plot, which adds vertical lines extending from the top and bottom of the plot to, for example, the maximum and minimum values.
Key Terms
- regression
-
An analytic method to measure the association of one or more independent variables with a dependent variable.
- box-and-whisker plot
-
a convenient way of graphically depicting groups of numerical data through their quartiles
A single statistic tells only part of a dataset’s story. The mean is one perspective; the median yet another. When we explore relationships between multiple variables, even more statistics arise, such as the coefficient estimates in a regression model or the Cochran-Maentel-Haenszel test statistic in partial contingency tables. A multitude of statistics are available to summarize and test data.
Our ultimate goal in statistics is not to summarize the data, it is to fully understand their complex relationships. A well designed statistical graphic helps us explore, and perhaps understand, these relationships. A box plot (also called a box and whisker diagram) is a simple visual representation of key features of a univariate sample.
The box lies on a vertical axis in the range of the sample. Typically, a top to the box is placed at the first quartile, the bottom at the third quartile. The width of the box is arbitrary, as there is no x-axis. In between the top and bottom of the box is some representation of central tendency. A common version is to place a horizontal line at the median, dividing the box into two. Additionally, a star or asterisk is placed at the mean value, centered in the box in the horizontal direction.
Another common extension of the box model is the ‘box-and-whisker’ plot , which adds vertical lines extending from the top and bottom of the plot to, for example, the maximum and minimum values. Alternatively, the whiskers could extend to the 2.5 and 97.5 percentiles. Finally, it is common in the box-and-whisker plot to show outliers (however defined) with asterisks at the individual values beyond the ends of the whiskers.

Box-and-Whisker Plot
Box plot of data from the Michelson-Morley Experiment, which attempted to detect the relative motion of matter through the stationary luminiferous aether.

Box Plot
Box plot of data from the Michelson-Morley Experiment.
5.4: Further Considerations for Data
5.4.1: The Sample Average
The sample average/mean can be calculated taking the sum of every piece of data and dividing that sum by the total number of data points.
Learning Objective
Distinguish the sample mean from the population mean.
Key Points
- The sample mean makes a good estimator of the population mean, as its expected value is equal to the population mean. The law of large numbers dictates that the larger the size of the sample, the more likely it is that the sample mean will be close to the population mean.
- The sample mean of a population is a random variable, not a constant, and consequently it will have its own distribution.
- The mean is the arithmetic average of a set of values, or distribution; however, for skewed distributions, the mean is not necessarily the same as the middle value (median), or the most likely (mode).
Key Terms
- random variable
-
a quantity whose value is random and to which a probability distribution is assigned, such as the possible outcome of a roll of a die
- finite
-
limited, constrained by bounds, having an end
Sample Average vs. Population Average
The sample average (also called the sample mean) is often referred to as the arithmetic mean of a sample, or simply,
(pronounced “x bar”). The mean of a population is denoted
, known as the population mean. The sample mean makes a good estimator of the population mean, as its expected value is equal to the population mean. The sample mean of a population is a random variable, not a constant, and consequently it will have its own distribution. For a random sample of
observations from a normally distributed population, the sample mean distribution is:
For a finite population, the population mean of a property is equal to the arithmetic mean of the given property while considering every member of the population. For example, the population mean height is equal to the sum of the heights of every individual divided by the total number of individuals.The sample mean may differ from the population mean, especially for small samples. The law of large numbers dictates that the larger the size of the sample, the more likely it is that the sample mean will be close to the population mean.
Calculation of the Sample Mean
The arithmetic mean is the “standard” average, often simply called the “mean”. It can be calculated taking the sum of every piece of data and dividing that sum by the total number of data points:
For example, the arithmetic mean of five values: 4, 36, 45, 50, 75 is:
The mean may often be confused with the median, mode or range. The mean is the arithmetic average of a set of values, or distribution; however, for skewed distributions, the mean is not necessarily the same as the middle value (median), or the most likely (mode). For example, mean income is skewed upwards by a small number of people with very large incomes, so that the majority have an income lower than the mean. By contrast, the median income is the level at which half the population is below and half is above. The mode income is the most likely income, and favors the larger number of people with lower incomes. The median or mode are often more intuitive measures of such data .

Measures of Central Tendency
This graph shows where the mean, median, and mode fall in two different distributions (one is slightly skewed left and one is highly skewed right).
5.4.2: Which Standard Deviation (SE)?
Although they are often used interchangeably, the standard deviation and the standard error are slightly different.
Learning Objective
Differentiate between standard deviation and standard error.
Key Points
- Standard error is an estimate of how close to the population mean your sample mean is likely to be, whereas standard deviation is the degree to which individuals within the sample differ from the sample mean.
- Standard deviation (represented by the symbol sigma, σ) shows how much variation or dispersion exists from the average (mean), or expected value.
- The standard error is the standard deviation of the sampling distribution of a statistic, such as the mean.
- Standard error should decrease with larger sample sizes, as the estimate of the population mean improves. Standard deviation will be unaffected by sample size.
Key Terms
- standard error
-
A measure of how spread out data values are around the mean, defined as the square root of the variance.
- central limit theorem
-
The theorem that states: If the sum of independent identically distributed random variables has a finite variance, then it will be (approximately) normally distributed.
- sample mean
-
the mean of a sample of random variables taken from the entire population of those variables
The standard error is the standard deviation of the sampling distribution of a statistic. The term may also be used to refer to an estimate of that standard deviation, derived from a particular sample used to compute the estimate.
For example, the sample mean is the usual estimator of a population mean. However, different samples drawn from that same population would in general have different values of the sample mean. The standard error of the mean (i.e., of using the sample mean as a method of estimating the population mean) is the standard deviation of those sample means over all possible samples (of a given size) drawn from the population. Secondly, the standard error of the mean can refer to an estimate of that standard deviation, computed from the sample of data being analyzed at the time.
In scientific and technical literature, experimental data is often summarized either using the mean and standard deviation or the mean with the standard error. This often leads to confusion about their interchangeability. However, the mean and standard deviation are descriptive statistics, whereas the mean and standard error describes bounds on a random sampling process. Despite the small difference in equations for the standard deviation and the standard error, this small difference changes the meaning of what is being reported from a description of the variation in measurements to a probabilistic statement about how the number of samples will provide a better bound on estimates of the population mean, in light of the central limit theorem. Put simply, standard error is an estimate of how close to the population mean your sample mean is likely to be, whereas standard deviation is the degree to which individuals within the sample differ from the sample mean. Standard error should decrease with larger sample sizes, as the estimate of the population mean improves. Standard deviation will be unaffected by sample size.

Standard Deviation
This is an example of two sample populations with the same mean and different standard deviations. The red population has mean 100 and SD 10; the blue population has mean 100 and SD 50.
5.4.3: Estimating the Accuracy of an Average
The standard error of the mean is the standard deviation of the sample mean’s estimate of a population mean.
Learning Objective
Evaluate the accuracy of an average by finding the standard error of the mean.
Key Points
- Any measurement is subject to error by chance, which means that if the measurement was taken again it could possibly show a different value.
- In general terms, the standard error is the standard deviation of the sampling distribution of a statistic.
- The standard error of the mean is usually estimated by the sample estimate of the population standard deviation (sample standard deviation) divided by the square root of the sample size.
- The standard error and standard deviation of small samples tend to systematically underestimate the population standard error and deviations because the standard error of the mean is a biased estimator of the population standard error.
- The standard error is an estimate of how close the population mean will be to the sample mean, whereas standard deviation is the degree to which individuals within the sample differ from the sample mean.
Key Terms
- standard error
-
A measure of how spread out data values are around the mean, defined as the square root of the variance.
- confidence interval
-
A type of interval estimate of a population parameter used to indicate the reliability of an estimate.
- central limit theorem
-
The theorem that states: If the sum of independent identically distributed random variables has a finite variance, then it will be (approximately) normally distributed.
Any measurement is subject to error by chance, meaning that if the measurement was taken again, it could possibly show a different value. We calculate the standard deviation in order to estimate the chance error for a single measurement. Taken further, we can calculate the chance error of the sample mean to estimate its accuracy in relation to the overall population mean.
Standard Error
In general terms, the standard error is the standard deviation of the sampling distribution of a statistic. The term may also be used to refer to an estimate of that standard deviation, derived from a particular sample used to compute the estimate. For example, the sample mean is the standard estimator of a population mean. However, different samples drawn from that same population would, in general, have different values of the sample mean.

Standard Deviation as Standard Error
For a value that is sampled with an unbiased normally distributed error, the graph depicts the proportion of samples that would fall between 0, 1, 2, and 3 standard deviations above and below the actual value.
The standard error of the mean (i.e., standard error of using the sample mean as a method of estimating the population mean) is the standard deviation of those sample means over all possible samples (of a given size) drawn from the population. Secondly, the standard error of the mean can refer to an estimate of that standard deviation, computed from the sample of data being analyzed at the time.
In practical applications, the true value of the standard deviation (of the error) is usually unknown. As a result, the term standard error is often used to refer to an estimate of this unknown quantity. In such cases, it is important to clarify one’s calculations, and take proper account of the fact that the standard error is only an estimate.
Standard Error of the Mean
As mentioned, the standard error of the mean (SEM) is the standard deviation of the sample-mean’s estimate of a population mean. It can also be viewed as the standard deviation of the error in the sample mean relative to the true mean, since the sample mean is an unbiased estimator. Generally, the SEM is the sample estimate of the population standard deviation (sample standard deviation) divided by the square root of the sample size:
Where s is the sample standard deviation (i.e., the sample-based estimate of the standard deviation of the population), and
is the size (number of observations) of the sample. This estimate may be compared with the formula for the true standard deviation of the sample mean:
Where
is the standard deviation of the population. Note that the standard error and the standard deviation of small samples tend to systematically underestimate the population standard error and deviations because the standard error of the mean is a biased estimator of the population standard error. For example, with
, the underestimate is about 25%, but for
, the underestimate is only 5%. As a practical result, decreasing the uncertainty in a mean value estimate by a factor of two requires acquiring four times as many observations in the sample. Decreasing standard error by a factor of ten requires a hundred times as many observations.
Assumptions and Usage
If the data are assumed to be normally distributed, quantiles of the normal distribution and the sample mean and standard error can be used to calculate approximate confidence intervals for the mean. In particular, the standard error of a sample statistic (such as sample mean) is the estimated standard deviation of the error in the process by which it was generated. In other words, it is the standard deviation of the sampling distribution of the sample statistic.
Standard errors provide simple measures of uncertainty in a value and are often used for the following reasons:
- If the standard error of several individual quantities is known, then the standard error of some function of the quantities can be easily calculated in many cases.
- Where the probability distribution of the value is known, it can be used to calculate a good approximation to an exact confidence interval.
- Where the probability distribution is unknown, relationships of inequality can be used to calculate a conservative confidence interval.
- As the sample size tends to infinity, the central limit theorem guarantees that the sampling distribution of the mean is asymptotically normal.
5.4.4: Chance Models
A stochastic model is used to estimate probability distributions of potential outcomes by allowing for random variation in one or more inputs over time.
Learning Objective
Support the idea that stochastic modeling provides a better representation of real life by building randomness into a simulation.
Key Points
- Accurately determining the standard error of the mean depends on the presence of chance.
- Stochastic modeling builds volatility and variability (randomness) into a simulation and, therefore, provides a better representation of real life from more angles.
- Stochastic models help to assess the interactions between variables and are useful tools to numerically evaluate quantities.
Key Terms
- Monte Carlo simulation
-
a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results–i.e., by running simulations many times over in order to calculate those same probabilities
- stochastic
-
random; randomly determined
The calculation of the standard error of the mean for repeated measurements is easily carried out on a data set; however, this method for determining error is only viable when the data varies as if drawing a name out of a hat. In other words, the data should be completely random, and should not show a trend or pattern over time. Therefore, accurately determining the standard error of the mean depends on the presence of chance.
Stochastic Modeling
“Stochastic” means being or having a random variable. A stochastic model is a tool for estimating probability distributions of potential outcomes by allowing for random variation in one or more inputs over time. The random variation is usually based on fluctuations observed in historical data for a selected period using standard time-series techniques. Distributions of potential outcomes are derived from a large number of simulations (stochastic projections) which reflect the random variation in the input(s).
In order to understand stochastic modeling, consider the example of an insurance company projecting potential claims. Like any other company, an insurer has to show that its assets exceed its liabilities to be solvent. In the insurance industry, however, assets and liabilities are not known entities. They depend on how many policies result in claims, inflation from now until the claim, investment returns during that period, and so on. So the valuation of an insurer involves a set of projections, looking at what is expected to happen, and thus coming up with the best estimate for assets and liabilities.
A stochastic model, in the case of the insurance company, would be to set up a projection model which looks at a single policy, an entire portfolio, or an entire company. But rather than setting investment returns according to their most likely estimate, for example, the model uses random variations to look at what investment conditions might be like. Based on a set of random outcomes, the experience of the policy/portfolio/company is projected, and the outcome is noted. This is done again with a new set of random variables. In fact, this process is repeated thousands of times.
At the end, a distribution of outcomes is available which shows not only the most likely estimate but what ranges are reasonable, too. The most likely estimate is given by the center of mass of the distribution curve (formally known as the probability density function), which is typically also the mode of the curve. Stochastic modeling builds volatility and variability (randomness) into a simulation and, therefore, provides a better representation of real life from more angles.
Numerical Evaluations of Quantities
Stochastic models help to assess the interactions between variables and are useful tools to numerically evaluate quantities, as they are usually implemented using Monte Carlo simulation techniques .

Monte Carlo Simulation
Monte Carlo simulation (10,000 points) of the distribution of the sample mean of a circular normal distribution for 3 measurements.
While there is an advantage here, in estimating quantities that would otherwise be difficult to obtain using analytical methods, a disadvantage is that such methods are limited by computing resources as well as simulation error. Below are some examples:
Means
Using statistical notation, it is a well-known result that the mean of a function,
, of a random variable,
, is not necessarily the function of the mean of
. For example, in finance, applying the best estimate (defined as the mean) of investment returns to discount a set of cash flows will not necessarily give the same result as assessing the best estimate to the discounted cash flows. A stochastic model would be able to assess this latter quantity with simulations.
Percentiles
This idea is seen again when one considers percentiles. When assessing risks at specific percentiles, the factors that contribute to these levels are rarely at these percentiles themselves. Stochastic models can be simulated to assess the percentiles of the aggregated distributions.
Truncations and Censors
Truncating and censoring of data can also be estimated using stochastic models. For instance, applying a non-proportional reinsurance layer to the best estimate losses will not necessarily give us the best estimate of the losses after the reinsurance layer. In a simulated stochastic model, the simulated losses can be made to “pass through” the layer and the resulting losses are assessed appropriately.
5.4.5: The Gauss Model
The normal (Gaussian) distribution is a commonly used distribution that can be used to display the data in many real life scenarios.
Learning Objective
Explain the importance of the Gauss model in terms of the central limit theorem.
Key Points
- If
and
, the distribution is called the standard normal distribution or the unit normal distribution, and a random variable with that distribution is a standard normal deviate. - It is symmetric around the point
, which is at the same time the mode, the median and the mean of the distribution. - The Gaussian distribution is sometimes informally called the bell curve. However, there are many other distributions that are bell-shaped as well.
- About 68% of values drawn from a normal distribution are within one standard deviation σ away from the mean; about 95% of the values lie within two standard deviations; and about 99.7% are within three standard deviations. This fact is known as the 68-95-99.7 (empirical) rule, or the 3-sigma rule.
Key Term
- central limit theorem
-
The theorem that states: If the sum of independent identically distributed random variables has a finite variance, then it will be (approximately) normally distributed.
The Normal (Gaussian) Distribution
In probability theory, the normal (or Gaussian) distribution is a continuous probability distribution, defined by the formula:
The parameter
in this formula is the mean or expectation of the distribution (and also its median and mode). The parameter
is its standard deviation; its variance is therefore
. A random variable with a Gaussian distribution is said to be normally distributed and is called a normal deviate.
If
and
, the distribution is called the standard normal distribution or the unit normal distribution, and a random variable with that distribution is a standard normal deviate.
Importance of the Normal Distribution
Normal distributions are extremely important in statistics, and are often used in the natural and social sciences for real-valued random variables whose distributions are not known. One reason for their popularity is the central limit theorem, which states that, under mild conditions, the mean of a large number of random variables independently drawn from the same distribution is distributed approximately normally, irrespective of the form of the original distribution. Thus, physical quantities that are expected to be the sum of many independent processes (such as measurement errors) often have a distribution very close to normal. Another reason is that a large number of results and methods (such as propagation of uncertainty and least squares parameter fitting) can be derived analytically, in explicit form, when the relevant variables are normally distributed.
The normal distribution is symmetric about its mean, and is non-zero over the entire real line. As such it may not be a suitable model for variables that are inherently positive or strongly skewed, such as the weight of a person or the price of a share. Such variables may be better described by other distributions, such as the log-normal distribution or the Pareto distribution.
The normal distribution is also practically zero once the value
lies more than a few standard deviations away from the mean. Therefore, it may not be appropriate when one expects a significant fraction of outliers, values that lie many standard deviations away from the mean. Least-squares and other statistical inference methods which are optimal for normally distributed variables often become highly unreliable. In those cases, one assumes a more heavy-tailed distribution, and the appropriate robust statistical inference methods.
The Gaussian distribution is sometimes informally called the bell curve. However, there are many other distributions that are bell-shaped (such as Cauchy’s, Student’s, and logistic). The terms Gaussian function and Gaussian bell curve are also ambiguous since they sometimes refer to multiples of the normal distribution whose integral is not 1; that is, for arbitrary positive constants
,
and
.
Properties of the Normal Distribution
The normal distribution
, with any mean
and any positive deviation
, has the following properties:
- It is symmetric around the point
, which is at the same time the mode, the median and the mean of the distribution. - It is unimodal: its first derivative is positive for
, negative for
, and zero only at
. - It has two inflection points (where the second derivative of
is zero), located one standard deviation away from the mean, namely at
and
. - About 68% of values drawn from a normal distribution are within one standard deviation
away from the mean; about 95% of the values lie within two standard deviations; and about 99.7% are within three standard deviations. This fact is known as the 68-95-99.7 (empirical) rule, or the 3-sigma rule .
Notation
The normal distribution is also often denoted by
. Thus when a random variable
is distributed normally with mean
and variance
, we write
5.4.6: Comparing Two Sample Averages
Student’s t-test is used in order to compare two independent sample means.
Learning Objective
Contrast two sample means by standardizing their difference to find a t-score test statistic.
Key Points
- Very different sample means can occur by chance if there is great variation among the individual samples.
- In order to account for the variation, we take the difference of the sample means and divide by the standard error in order to standardize the difference, resulting in a t-score test statistic.
- The independent samples t-test is used when two separate sets of independent and identically distributed samples are obtained, one from each of the two populations being compared.
- Paired samples t-tests typically consist of a sample of matched pairs of similar units or one group of units that has been tested twice (a “repeated measures” t-test).
- An overlapping samples t-test is used when there are paired samples with data missing in one or the other samples.
Key Terms
- null hypothesis
-
A hypothesis set up to be refuted in order to support an alternative hypothesis; presumed true until statistical evidence in the form of a hypothesis test indicates otherwise.
- Student’s t-distribution
-
A distribution that arises when the population standard deviation is unknown and has to be estimated from the data; originally derived by William Sealy Gosset (who wrote under the pseudonym “Student”).
The comparison of two sample means is very common. The difference between the two samples depends on both the means and the standard deviations. Very different means can occur by chance if there is great variation among the individual samples. In order to account for the variation, we take the difference of the sample means,
,
and divide by the standard error in order to standardize the difference. The result is a t-score test statistic.
t-Test for Two Means
Although the t-test will be explained in great detail later in this textbook, it is important for the reader to have a basic understanding of its function in regard to comparing two sample means. A t-test is any statistical hypothesis test in which the test statistic follows Student’s t distribution, as shown in , if the null hypothesis is supported. It can be used to determine if two sets of data are significantly different from each other.

Student t Distribution
This is a plot of the Student t Distribution for various degrees of freedom.
In the t-test comparing the means of two independent samples, the following assumptions should be met:
- Each of the two populations being compared should follow a normal distribution.
- If using Student’s original definition of the t-test, the two populations being compared should have the same variance. If the sample sizes in the two groups being compared are equal, Student’s original t-test is highly robust to the presence of unequal variances.
- The data used to carry out the test should be sampled independently from the populations being compared. This is, in general, not testable from the data, but if the data are known to be dependently sampled (i.e., if they were sampled in clusters), then the classical t-tests discussed here may give misleading results.
Two-sample t-tests for a difference in mean involve independent samples, paired samples and overlapping samples. The independent samples t-test is used when two separate sets of independent and identically distributed samples are obtained, one from each of the two populations being compared. For example, suppose we are evaluating the effects of a medical treatment. We enroll 100 subjects into our study, then randomize 50 subjects to the treatment group and 50 subjects to the control group. In this case, we have two independent samples and would use the unpaired form of the t-test.
Paired sample t-tests typically consist of a sample of matched pairs of similar units or one group of units that has been tested twice (a “repeated measures” t-test). A typical example of the repeated measures t-test would be where subjects are tested prior to a treatment (say, for high blood pressure) and the same subjects are tested again after treatment with a blood-pressure lowering medication. By comparing the same patient’s numbers before and after treatment, we are effectively using each patient as their own control.
An overlapping sample t-test is used when there are paired samples with data missing in one or the other samples. These tests are widely used in commercial survey research (e.g., by polling companies) and are available in many standard crosstab software packages.
5.4.7: Odds Ratios
The odds of an outcome is the ratio of the expected number of times the event will occur to the expected number of times the event will not occur.
Learning Objective
Define the odds ratio and demonstrate its computation.
Key Points
- The odds ratio is one way to quantify how strongly having or not having the property
is associated with having or not having the property
in a population. - The odds ratio is a measure of effect size, describing the strength of association or non-independence between two binary data values.
- To compute the odds ratio, we 1) compute the odds that an individual in the population has
given that he or she has
, 2) compute the odds that an individual in the population has
given that he or she does not have
and 3) divide the first odds by the second odds. - If the odds ratio is greater than one, then having
is associated with having
in the sense that having
raises the odds of having
.
Key Terms
- logarithm
-
for a number
$x$ , the power to which a given base number must be raised in order to obtain$x$ - odds
-
the ratio of the probabilities of an event happening to that of it not happening
The odds of an outcome is the ratio of the expected number of times the event will occur to the expected number of times the event will not occur. Put simply, the odds are the ratio of the probability of an event occurring to the probability of no event.
An odds ratio is the ratio of two odds. Imagine each individual in a population either does or does not have a property
, and also either does or does not have a property
. For example,
might be “has high blood pressure,” and
might be “drinks more than one alcoholic drink a day.” The odds ratio is one way to quantify how strongly having or not having the property
is associated with having or not having the property
in a population. In order to compute the odds ratio, one follows three steps:
- Compute the odds that an individual in the population has
given that he or she has
(probability of
given
divided by the probability of not-
given
). - Compute the odds that an individual in the population has
given that he or she does not have
. - Divide the first odds by the second odds to obtain the odds ratio.
If the odds ratio is greater than one, then having
is associated with having
in the sense that having
raises (relative to not having
) the odds of having
. Note that this is not enough to establish that
is a contributing cause of
. It could be that the association is due to a third property,
, which is a contributing cause of both
and
.
In more technical language, the odds ratio is a measure of effect size, describing the strength of association or non-independence between two binary data values. It is used as a descriptive statistic and plays an important role in logistic regression.
Example
Suppose that in a sample of
men
drank wine in the previous week, while in a sample of
women only
drank wine in the same period. The odds of a man drinking wine are
to
(or
) while the odds of a woman drinking wine are only
to
(or
). The odds ratio is thus
(or
) showing that men are much more likely to drink wine than women. The detailed calculation is:
This example also shows how odds ratios are sometimes sensitive in stating relative positions. In this sample men are
times more likely to have drunk wine than women, but have
times the odds. The logarithm of the odds ratio—the difference of the logits of the probabilities—tempers this effect and also makes the measure symmetric with respect to the ordering of groups. For example, using natural logarithms, an odds ratio of
maps to
, and an odds ratio of
maps to
.

Odds Ratios
A graph showing how the log odds ratio relates to the underlying probabilities of the outcome
occurring in two groups, denoted
and
. The log odds ratio shown here is based on the odds for the event occurring in group
relative to the odds for the event occurring in group
. Thus, when the probability of
occurring in group
is greater than the probability of
occurring in group
, the odds ratio is greater than
, and the log odds ratio is greater than
.
5.4.8: When Does the Z-Test Apply?
A
-test is a test for which the distribution of the test statistic under the null hypothesis can be approximated by a normal distribution.
Learning Objective
Identify how sample size contributes to the appropriateness and accuracy of a
Key Points
- The term
-test is often used to refer specifically to the one-sample location test comparing the mean of a set of measurements to a given constant. - To calculate the standardized statistic
, we need to either know or have an approximate value for
σ2, from which we can calculate
. - For a
-test to be applicable, nuisance parameters should be known, or estimated with high accuracy. - For a
-test to be applicable, the test statistic should follow a normal distribution.
Key Terms
- null hypothesis
-
A hypothesis set up to be refuted in order to support an alternative hypothesis; presumed true until statistical evidence in the form of a hypothesis test indicates otherwise.
- nuisance parameters
-
any parameter that is not of immediate interest but which must be accounted for in the analysis of those parameters which are of interest; the classic example of a nuisance parameter is the variance
$\sigma^2$ , of a normal distribution, when the mean,$\mu$ , is of primary interest
-test
A
-test is any statistical test for which the distribution of the test statistic under the null hypothesis can be approximated by a normal distribution. Because of the central limit theorem, many test statistics are approximately normally distributed for large samples. For each significance level, the
-test has a single critical value (for example,
for 5% two tailed) which makes it more convenient than the Student’s t-test which has separate critical values for each sample size. Therefore, many statistical tests can be conveniently performed as approximate
-tests if the sample size is large or the population variance known. If the population variance is unknown (and therefore has to be estimated from the sample itself) and the sample size is not large (
), the Student
-test may be more appropriate.
If
is a statistic that is approximately normally distributed under the null hypothesis, the next step in performing a
-test is to estimate the expected value
of
under the null hypothesis, and then obtain an estimate
of the standard deviation of
. We then calculate the standard score
, from which one-tailed and two-tailed
-values can be calculated as
(for upper-tailed tests),
(for lower-tailed tests) and
(for two-tailed tests) where
is the standard normal cumulative distribution function.
Use in Location Testing
The term
-test is often used to refer specifically to the one-sample location test comparing the mean of a set of measurements to a given constant. If the observed data
are uncorrelated, have a common mean
, and have a common variance
, then the sample average
has mean
and variance
. If our null hypothesis is that the mean value of the population is a given number
, we can use
as a test-statistic, rejecting the null hypothesis if
is large.
To calculate the standardized statistic
, we need to either know or have an approximate value for
, from which we can calculate
. In some applications,
is known, but this is uncommon. If the sample size is moderate or large, we can substitute the sample variance for
, giving a plug-in test. The resulting test will not be an exact
-test since the uncertainty in the sample variance is not accounted for—however, it will be a good approximation unless the sample size is small. A
-test can be used to account for the uncertainty in the sample variance when the sample size is small and the data are exactly normal. There is no universal constant at which the sample size is generally considered large enough to justify use of the plug-in test. Typical rules of thumb range from 20 to 50 samples. For larger sample sizes, the
-test procedure gives almost identical
-values as the
-test procedure. The following formula converts a random variable
to the standard
:
Conditions
For the
-test to be applicable, certain conditions must be met:
- Nuisance parameters should be known, or estimated with high accuracy (an example of a nuisance parameter would be the standard deviation in a one-sample location test).
-tests focus on a single parameter, and treat all other unknown parameters as being fixed at their true values. In practice, due to Slutsky’s theorem, “plugging in” consistent estimates of nuisance parameters can be justified. However if the sample size is not large enough for these estimates to be reasonably accurate, the
-test may not perform well. - The test statistic should follow a normal distribution. Generally, one appeals to the central limit theorem to justify assuming that a test statistic varies normally. There is a great deal of statistical research on the question of when a test statistic varies approximately normally. If the variation of the test statistic is strongly non-normal, a
-test should not be used.
Chapter 4: Frequency Distributions
4.1: Frequency Distributions for Quantitative Data
4.1.1: Guidelines for Plotting Frequency Distributions
The frequency distribution of events is the number of times each event occurred in an experiment or study.
Learning Objective
Define statistical frequency and illustrate how it can be depicted graphically.
Key Points
- Frequency distributions can be displayed in a table, histogram, line graph, dot plot, or a pie chart, just to name a few.
- A histogram is a graphical representation of tabulated frequencies, shown as adjacent rectangles, erected over discrete intervals (bins), with an area equal to the frequency of the observations in the interval.
- There is no “best” number of bins, and different bin sizes can reveal different features of the data.
- Frequency distributions can be displayed in a table, histogram, line graph, dot plot, or a pie chart, to just name a few.
Key Terms
- frequency
-
number of times an event occurred in an experiment (absolute frequency)
- histogram
-
a representation of tabulated frequencies, shown as adjacent rectangles, erected over discrete intervals (bins), with an area equal to the frequency of the observations in the interval
In statistics, the frequency (or absolute frequency) of an event is the number of times the event occurred in an experiment or study. These frequencies are often graphically represented in histograms. The relative frequency (or empirical probability) of an event refers to the absolute frequency normalized by the total number of events. The values of all events can be plotted to produce a frequency distribution.
A histogram is a graphical representation of tabulated frequencies , shown as adjacent rectangles, erected over discrete intervals (bins), with an area equal to the frequency of the observations in the interval. The height of a rectangle is also equal to the frequency density of the interval, i.e., the frequency divided by the width of the interval. The total area of the histogram is equal to the number of data. An example of the frequency distribution of letters of the alphabet in the English language is shown in the histogram in .

Letter frequency in the English language
A typical distribution of letters in English language text.
A histogram may also be normalized displaying relative frequencies. It then shows the proportion of cases that fall into each of several categories, with the total area equaling 1. The categories are usually specified as consecutive, non-overlapping intervals of a variable. The categories (intervals) must be adjacent, and often are chosen to be of the same size. The rectangles of a histogram are drawn so that they touch each other to indicate that the original variable is continuous.
There is no “best” number of bins, and different bin sizes can reveal different features of the data. Some theoreticians have attempted to determine an optimal number of bins, but these methods generally make strong assumptions about the shape of the distribution. Depending on the actual data distribution and the goals of the analysis, different bin widths may be appropriate, so experimentation is usually needed to determine an appropriate width.
4.1.2: Outliers
In statistics, an outlier is an observation that is numerically distant from the rest of the data.
Learning Objective
Discuss outliers in terms of their causes and consequences, identification, and exclusion.
Key Points
- Outliers can occur by chance, by human error, or by equipment malfunction.
- Outliers may be indicative of a non-normal distribution, or they may just be natural deviations that occur in a large sample.
- Unless it can be ascertained that the deviation is not significant, it is not wise to ignore the presence of outliers.
- There is no rigid mathematical definition of what constitutes an outlier; thus, determining whether or not an observation is an outlier is ultimately a subjective experience.
Key Terms
- skewed
-
Biased or distorted (pertaining to statistics or information).
- standard deviation
-
a measure of how spread out data values are around the mean, defined as the square root of the variance
- interquartile range
-
The difference between the first and third quartiles; a robust measure of sample dispersion.
What is an Outlier?
In statistics, an outlier is an observation that is numerically distant from the rest of the data. Outliers can occur by chance in any distribution, but they are often indicative either of measurement error or of the population having a heavy-tailed distribution. In the former case, one wishes to discard the outliers or use statistics that are robust against them. In the latter case, outliers indicate that the distribution is skewed and that one should be very cautious in using tools or intuitions that assume a normal distribution.

Outliers
This box plot shows where the US states fall in terms of their size. Rhode Island, Texas, and Alaska are outside the normal data range, and therefore are considered outliers in this case.
In most larger samplings of data, some data points will be further away from the sample mean than what is deemed reasonable. This can be due to incidental systematic error or flaws in the theory that generated an assumed family of probability distributions, or it may be that some observations are far from the center of the data. Outlier points can therefore indicate faulty data, erroneous procedures, or areas where a certain theory might not be valid. However, in large samples, a small number of outliers is to be expected, and they typically are not due to any anomalous condition.
Outliers, being the most extreme observations, may include the sample maximum or sample minimum, or both, depending on whether they are extremely high or low. However, the sample maximum and minimum are not always outliers because they may not be unusually far from other observations.
Interpretations of statistics derived from data sets that include outliers may be misleading. For example, imagine that we calculate the average temperature of 10 objects in a room. Nine of them are between 20° and 25° Celsius, but an oven is at 175°C. In this case, the median of the data will be between 20° and 25°C, but the mean temperature will be between 35.5° and 40 °C. The median better reflects the temperature of a randomly sampled object than the mean; however, interpreting the mean as “a typical sample”, equivalent to the median, is incorrect. This case illustrates that outliers may be indicative of data points that belong to a different population than the rest of the sample set. Estimators capable of coping with outliers are said to be robust. The median is a robust statistic, while the mean is not.
Causes for Outliers
Outliers can have many anomalous causes. For example, a physical apparatus for taking measurements may have suffered a transient malfunction, or there may have been an error in data transmission or transcription. Outliers can also arise due to changes in system behavior, fraudulent behavior, human error, instrument error or simply through natural deviations in populations. A sample may have been contaminated with elements from outside the population being examined. Alternatively, an outlier could be the result of a flaw in the assumed theory, calling for further investigation by the researcher.
Unless it can be ascertained that the deviation is not significant, it is ill-advised to ignore the presence of outliers. Outliers that cannot be readily explained demand special attention.
Identifying Outliers
There is no rigid mathematical definition of what constitutes an outlier. Thus, determining whether or not an observation is an outlier is ultimately a subjective exercise. Model-based methods, which are commonly used for identification, assume that the data is from a normal distribution and identify observations which are deemed “unlikely” based on mean and standard deviation. Other methods flag observations based on measures such as the interquartile range (IQR). For example, some people use the
rule. This defines an outlier to be any observation that falls
below the first quartile or any observation that falls
above the third quartile.
Working With Outliers
Deletion of outlier data is a controversial practice frowned on by many scientists and science instructors. While mathematical criteria provide an objective and quantitative method for data rejection, they do not make the practice more scientifically or methodologically sound — especially in small sets or where a normal distribution cannot be assumed. Rejection of outliers is more acceptable in areas of practice where the underlying model of the process being measured and the usual distribution of measurement error are confidently known. An outlier resulting from an instrument reading error may be excluded, but it is desirable that the reading is at least verified.
Even when a normal distribution model is appropriate to the data being analyzed, outliers are expected for large sample sizes and should not automatically be discarded if that is the case. The application should use a classification algorithm that is robust to outliers to model data with naturally occurring outlier points. Additionally, the possibility should be considered that the underlying distribution of the data is not approximately normal, but rather skewed.
4.1.3: Relative Frequency Distributions
A relative frequency is the fraction or proportion of times a value occurs in a data set.
Learning Objective
Define relative frequency and construct a relative frequency distribution.
Key Points
- To find the relative frequencies, divide each frequency by the total number of data points in the sample.
- Relative frequencies can be written as fractions, percents, or decimals. The column should add up to 1 (or 100%).
- The only difference between a relative frequency distribution graph and a frequency distribution graph is that the vertical axis uses proportional or relative frequency rather than simple frequency.
- Cumulative relative frequency (also called an ogive) is the accumulation of the previous relative frequencies.
Key Terms
- cumulative relative frequency
-
the accumulation of the previous relative frequencies
- relative frequency
-
the fraction or proportion of times a value occurs
- histogram
-
a representation of tabulated frequencies, shown as adjacent rectangles, erected over discrete intervals (bins), with an area equal to the frequency of the observations in the interval
What is a Relative Frequency Distribution?
A relative frequency is the fraction or proportion of times a value occurs. To find the relative frequencies, divide each frequency by the total number of data points in the sample. Relative frequencies can be written as fractions, percents, or decimals.
How to Construct a Relative Frequency Distribution
Constructing a relative frequency distribution is not that much different than from constructing a regular frequency distribution. The beginning process is the same, and the same guidelines must be used when creating classes for the data. Recall the following:
- Each data value should fit into one class only (classes are mutually exclusive).
- The classes should be of equal size.
- Classes should not be open-ended.
- Try to use between 5 and 20 classes.
Create the frequency distribution table, as you would normally. However, this time, you will need to add a third column. The first column should be labeled Class or Category. The second column should be labeled Frequency. The third column should be labeled Relative Frequency. Fill in your class limits in column one. Then, count the number of data points that fall in each class and write that number in column two.
Next, start to fill in the third column. The entries will be calculated by dividing the frequency of that class by the total number of data points. For example, suppose we have a frequency of 5 in one class, and there are a total of 50 data points. The relative frequency for that class would be calculated by the following:
You can choose to write the relative frequency as a decimal (0.10), as a fraction (
), or as a percent (10%). Since we are dealing with proportions, the relative frequency column should add up to 1 (or 100%). It may be slightly off due to rounding.
Relative frequency distributions is often displayed in histograms and in frequency polygons. The only difference between a relative frequency distribution graph and a frequency distribution graph is that the vertical axis uses proportional or relative frequency rather than simple frequency.
Relative Frequency Histogram
This graph shows a relative frequency histogram. Notice the vertical axis is labeled with percentages rather than simple frequencies.
Cumulative Relative Frequency Distributions
Just like we use cumulative frequency distributions when discussing simple frequency distributions, we often use cumulative frequency distributions when dealing with relative frequency as well. Cumulative relative frequency (also called an ogive) is the accumulation of the previous relative frequencies. To find the cumulative relative frequencies, add all the previous relative frequencies to the relative frequency for the current row.
4.1.4: Cumulative Frequency Distributions
A cumulative frequency distribution displays a running total of all the preceding frequencies in a frequency distribution.
Learning Objective
Define cumulative frequency and construct a cumulative frequency distribution.
Key Points
- To create a cumulative frequency distribution, start by creating a regular frequency distribution with one extra column added.
- To complete the cumulative frequency column, add all the frequencies at that class and all preceding classes.
- Cumulative frequency distributions are often displayed in histograms and in frequency polygons.
Key Terms
- histogram
-
a representation of tabulated frequencies, shown as adjacent rectangles, erected over discrete intervals (bins), with an area equal to the frequency of the observations in the interval
- frequency distribution
-
a representation, either in a graphical or tabular format, which displays the number of observations within a given interval
What is a Cumulative Frequency Distribution?
A cumulative frequency distribution is the sum of the class and all classes below it in a frequency distribution. Rather than displaying the frequencies from each class, a cumulative frequency distribution displays a running total of all the preceding frequencies.
How to Construct a Cumulative Frequency Distribution
Constructing a cumulative frequency distribution is not that much different than constructing a regular frequency distribution. The beginning process is the same, and the same guidelines must be used when creating classes for the data. Recall the following:
- Each data value should fit into one class only (classes are mutually exclusive).
- The classes should be of equal size.
- Classes should not be open-ended.
- Try to use between 5 and 20 classes.
Create the frequency distribution table, as you would normally. However, this time, you will need to add a third column. The first column should be labeled Class or Category. The second column should be labeled Frequency. The third column should be labeled Cumulative Frequency. Fill in your class limits in column one. Then, count the number of data points that falls in each class and write that number in column two.
Next, start to fill in the third column. The first entry will be the same as the first entry in the Frequency column. The second entry will be the sum of the first two entries in the Frequency column, the third entry will be the sum of the first three entries in the Frequency column, etc. The last entry in the Cumulative Frequency column should equal the number of total data points, if the math has been done correctly.
Graphical Displays of Cumulative Frequency Distributions
There are a number of ways in which cumulative frequency distributions can be displayed graphically. Histograms are common , as are frequency polygons . Frequency polygons are a graphical device for understanding the shapes of distributions. They serve the same purpose as histograms, but are especially helpful in comparing sets of data.
Frequency Polygon
This graph shows an example of a cumulative frequency polygon.

Frequency Histograms
This image shows the difference between an ordinary histogram and a cumulative frequency histogram.
4.1.5: Graphs for Quantitative Data
A plot is a graphical technique for representing a data set, usually as a graph showing the relationship between two or more variables.
Learning Objective
Identify common plots used in statistical analysis.
Key Points
- Graphical procedures such as plots are used to gain insight into a data set in terms of testing assumptions, model selection, model validation, estimator selection, relationship identification, factor effect determination, or outlier detection.
- Statistical graphics give insight into aspects of the underlying structure of the data.
- Graphs can also be used to solve some mathematical equations, typically by finding where two plots intersect.
Key Terms
- histogram
-
a representation of tabulated frequencies, shown as adjacent rectangles, erected over discrete intervals (bins), with an area equal to the frequency of the observations in the interval
- plot
-
a graph or diagram drawn by hand or produced by a mechanical or electronic device
- scatter plot
-
A type of display using Cartesian coordinates to display values for two variables for a set of data.
A plot is a graphical technique for representing a data set, usually as a graph showing the relationship between two or more variables. Graphs of functions are used in mathematics, sciences, engineering, technology, finance, and other areas where a visual representation of the relationship between variables would be useful. Graphs can also be used to read off the value of an unknown variable plotted as a function of a known one. Graphical procedures are also used to gain insight into a data set in terms of:
- testing assumptions,
- model selection,
- model validation,
- estimator selection,
- relationship identification,
- factor effect determination, or
- outlier detection.
Plots play an important role in statistics and data analysis. The procedures here can broadly be split into two parts: quantitative and graphical. Quantitative techniques are the set of statistical procedures that yield numeric or tabular output. Some examples of quantitative techniques include:
- hypothesis testing,
- analysis of variance,
- point estimates and confidence intervals, and
- least squares regression.
There are also many statistical tools generally referred to as graphical techniques which include:
- scatter plots ,
- histograms,
- probability plots,
- residual plots,
- box plots, and
- block plots.
Below are brief descriptions of some of the most common plots:
Scatter plot: This is a type of mathematical diagram using Cartesian coordinates to display values for two variables for a set of data. The data is displayed as a collection of points, each having the value of one variable determining the position on the horizontal axis and the value of the other variable determining the position on the vertical axis. This kind of plot is also called a scatter chart, scattergram, scatter diagram, or scatter graph.
Histogram: In statistics, a histogram is a graphical representation of the distribution of data. It is an estimate of the probability distribution of a continuous variable or can be used to plot the frequency of an event (number of times an event occurs) in an experiment or study.
Box plot: In descriptive statistics, a boxplot, also known as a box-and-whisker diagram, is a convenient way of graphically depicting groups of numerical data through their five-number summaries (the smallest observation, lower quartile (Q1), median (Q2), upper quartile (Q3), and largest observation). A boxplot may also indicate which observations, if any, might be considered outliers.
Scatter Plot
This is an example of a scatter plot, depicting the waiting time between eruptions and the duration of the eruption for the Old Faithful geyser in Yellowstone National Park, Wyoming, USA.
4.1.6: Typical Shapes
Distributions can be symmetrical or asymmetrical depending on how the data falls.
Learning Objective
Evaluate the shapes of symmetrical and asymmetrical frequency distributions.
Key Points
- A normal distribution is a symmetric distribution in which the mean and median are equal. Most data are clustered in the center.
- An asymmetrical distribution is said to be positively skewed (or skewed to the right) when the tail on the right side of the histogram is longer than the left side.
- An asymmetrical distribution is said to be negatively skewed (or skewed to the left) when the tail on the left side of the histogram is longer than the right side.
- Distributions can also be uni-modal, bi-modal, or multi-modal.
Key Terms
- skewness
-
A measure of the asymmetry of the probability distribution of a real-valued random variable; is the third standardized moment, defined as where is the third moment about the mean and is the standard deviation.
- empirical rule
-
That a normal distribution has 68% of its observations within one standard deviation of the mean, 95% within two, and 99.7% within three.
- standard deviation
-
a measure of how spread out data values are around the mean, defined as the square root of the variance
Distribution Shapes
In statistics, distributions can take on a variety of shapes. Considerations of the shape of a distribution arise in statistical data analysis, where simple quantitative descriptive statistics and plotting techniques, such as histograms, can lead to the selection of a particular family of distributions for modelling purposes.
Symmetrical Distributions
In a symmetrical distribution, the two sides of the distribution are mirror images of each other. A normal distribution is an example of a truly symmetric distribution of data item values. When a histogram is constructed on values that are normally distributed, the shape of the columns form a symmetrical bell shape. This is why this distribution is also known as a “normal curve” or “bell curve. ” In a true normal distribution, the mean and median are equal, and they appear in the center of the curve. Also, there is only one mode, and most of the data are clustered around the center. The more extreme values on either side of the center become more rare as distance from the center increases. About 68% of values lie within one standard deviation (σ) away from the mean, about 95% of the values lie within two standard deviations, and about 99.7% lie within three standard deviations . This is known as the empirical rule or the 3-sigma rule.
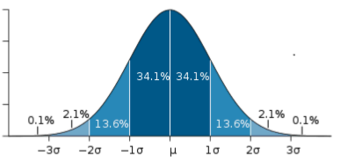
Normal Distribution
This image shows a normal distribution. About 68% of data fall within one standard deviation, about 95% fall within two standard deviations, and 99.7% fall within three standard deviations.
Asymmetrical Distributions
In an asymmetrical distribution, the two sides will not be mirror images of each other. Skewness is the tendency for the values to be more frequent around the high or low ends of the x-axis. When a histogram is constructed for skewed data, it is possible to identify skewness by looking at the shape of the distribution.
A distribution is said to be positively skewed (or skewed to the right) when the tail on the right side of the histogram is longer than the left side. Most of the values tend to cluster toward the left side of the x-axis (i.e., the smaller values) with increasingly fewer values at the right side of the x-axis (i.e., the larger values). In this case, the median is less than the mean .
Positively Skewed Distribution
This distribution is said to be positively skewed (or skewed to the right) because the tail on the right side of the histogram is longer than the left side.
A distribution is said to be negatively skewed (or skewed to the left) when the tail on the left side of the histogram is longer than the right side. Most of the values tend to cluster toward the right side of the x-axis (i.e., the larger values), with increasingly less values on the left side of the x-axis (i.e., the smaller values). In this case, the median is greater than the mean .
Negatively Skewed Distribution
This distribution is said to be negatively skewed (or skewed to the left) because the tail on the left side of the histogram is longer than the right side.
When data are skewed, the median is usually a more appropriate measure of central tendency than the mean.
Other Distribution Shapes
A uni-modal distribution occurs if there is only one “peak” (or highest point) in the distribution, as seen previously in the normal distribution. This means there is one mode (a value that occurs more frequently than any other) for the data. A bi-modal distribution occurs when there are two modes. Multi-modal distributions with more than two modes are also possible.
4.1.7: Z-Scores and Location in a Distribution
A
-score is the signed number of standard deviations an observation is above the mean of a distribution.
Learning Objective
Define
Key Points
- A positive
-score represents an observation above the mean, while a negative
-score represents an observation below the mean. - We obtain a
-score through a conversion process known as standardizing or normalizing. -
-scores are most frequently used to compare a sample to a standard normal deviate (standard normal distribution, with
and
). - While
-scores can be defined without assumptions of normality, they can only be defined if one knows the population parameters. -
-scores provide an assessment of how off-target a process is operating.
Key Terms
- Student’s t-statistic
-
a ratio of the departure of an estimated parameter from its notional value and its standard error
- z-score
-
The standardized value of observation
$x$ from a distribution that has mean$\mu$ and standard deviation$\sigma$ . - raw score
-
an original observation that has not been transformed to a
$z$ -score
A
-score is the signed number of standard deviations an observation is above the mean of a distribution. Thus, a positive
-score represents an observation above the mean, while a negative
-score represents an observation below the mean. We obtain a
-score through a conversion process known as standardizing or normalizing.
-scores are also called standard scores,
-values, normal scores or standardized variables. The use of “
” is because the normal distribution is also known as the “
distribution.”
-scores are most frequently used to compare a sample to a standard normal deviate (standard normal distribution, with
and
).
While
-scores can be defined without assumptions of normality, they can only be defined if one knows the population parameters. If one only has a sample set, then the analogous computation with sample mean and sample standard deviation yields the Student’s
-statistic.
Calculation From a Raw Score
A raw score is an original datum, or observation, that has not been transformed. This may include, for example, the original result obtained by a student on a test (i.e., the number of correctly answered items) as opposed to that score after transformation to a standard score or percentile rank. The
-score, in turn, provides an assessment of how off-target a process is operating.
The conversion of a raw score,
, to a
-score can be performed using the following equation:
where
is the mean of the population and
is the standard deviation of the population. The absolute value of
represents the distance between the raw score and the population mean in units of the standard deviation.
is negative when the raw score is below the mean and positive when the raw score is above the mean.
A key point is that calculating
requires the population mean and the population standard deviation, not the sample mean nor sample deviation. It requires knowing the population parameters, not the statistics of a sample drawn from the population of interest. However, in cases where it is impossible to measure every member of a population, the standard deviation may be estimated using a random sample.
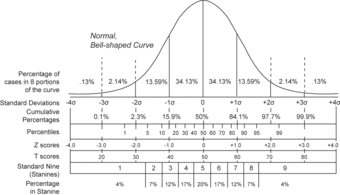
Normal Distribution and Scales
Shown here is a chart comparing the various grading methods in a normal distribution.
-scores for this standard normal distribution can be seen in between percentiles and
-scores.
4.2: Frequency Distributions for Qualitative Data
4.2.1: Describing Qualitative Data
Qualitative data is a categorical measurement expressed not in terms of numbers, but rather by means of a natural language description.
Learning Objective
Summarize the processes available to researchers that allow qualitative data to be analyzed similarly to quantitative data.
Key Points
- Observer impression is when expert or bystander observers examine the data, interpret it via forming an impression and report their impression in a structured and sometimes quantitative form.
- To discover patterns in qualitative data, one must try to find frequencies, magnitudes, structures, processes, causes, and consequences.
- The Ground Theory Method (GTM) is an inductive approach to research in which theories are generated solely from an examination of data rather than being derived deductively.
- Coding is an interpretive technique that both organizes the data and provides a means to introduce the interpretations of it into certain quantitative methods.
- Most coding requires the analyst to read the data and demarcate segments within it.
Key Terms
- nominal
-
Having values whose order is insignificant.
- ordinal
-
Of a number, indicating position in a sequence.
- qualitative analysis
-
The numerical examination and interpretation of observations for the purpose of discovering underlying meanings and patterns of relationships.
Qualitative data is a categorical measurement expressed not in terms of numbers, but rather by means of a natural language description. In statistics, it is often used interchangeably with “categorical” data. When there is not a natural ordering of the categories, we call these nominal categories. Examples might be gender, race, religion, or sport.
When the categories may be ordered, these are called ordinal variables. Categorical variables that judge size (small, medium, large, etc.) are ordinal variables. Attitudes (strongly disagree, disagree, neutral, agree, strongly agree) are also ordinal variables; however, we may not know which value is the best or worst of these issues. Note that the distance between these categories is not something we can measure.
Qualitative Analysis
Qualitative Analysis is the numerical examination and interpretation of observations for the purpose of discovering underlying meanings and patterns of relationships. The most common form of qualitative qualitative analysis is observer impression—when an expert or bystander observers examine the data, interpret it via forming an impression and report their impression in a structured and sometimes quantitative form.
An important first step in qualitative analysis and observer impression is to discover patterns. One must try to find frequencies, magnitudes, structures, processes, causes, and consequences. One method of this is through cross-case analysis, which is analysis that involves an examination of more than one case. Cross-case analysis can be further broken down into variable-oriented analysis and case-oriented analysis. Variable-oriented analysis is that which describes and/or explains a particular variable, while case-oriented analysis aims to understand a particular case or several cases by looking closely at the details of each.
The Ground Theory Method (GTM) is an inductive approach to research, introduced by Barney Glaser and Anselm Strauss, in which theories are generated solely from an examination of data rather than being derived deductively. A component of the Grounded Theory Method is the constant comparative method, in which observations are compared with one another and with the evolving inductive theory.
Four Stages of the Constant Comparative Method
- comparing incident application to each category
- integrating categories and their properties
- delimiting the theory
- writing theory
Other methods of discovering patterns include semiotics and conversation analysis. Semiotics is the study of signs and the meanings associated with them. It is commonly associated with content analysis. Conversation analysis is a meticulous analysis of the details of conversation, based on a complete transcript that includes pauses and other non-verbal communication.
Conceptualization and Coding
In quantitative analysis, it is usually obvious what the variables to be analyzed are, for example, race, gender, income, education, etc. Deciding what is a variable, and how to code each subject on each variable, is more difficult in qualitative data analysis.
Concept formation is the creation of variables (usually called themes) out of raw qualitative data. It is more sophisticated in qualitative data analysis. Casing is an important part of concept formation. It is the process of determining what represents a case. Coding is the actual transformation of qualitative data into themes.
More specifically, coding is an interpretive technique that both organizes the data and provides a means to introduce the interpretations of it into certain quantitative methods. Most coding requires the analyst to read the data and demarcate segments within it, which may be done at different times throughout the process. Each segment is labeled with a “code” – usually a word or short phrase that suggests how the associated data segments inform the research objectives. When coding is complete, the analyst prepares reports via a mix of: summarizing the prevalence of codes, discussing similarities and differences in related codes across distinct original sources/contexts, or comparing the relationship between one or more codes.
Some qualitative data that is highly structured (e.g., close-end responses from surveys or tightly defined interview questions) is typically coded without additional segmenting of the content. In these cases, codes are often applied as a layer on top of the data. Quantitative analysis of these codes is typically the capstone analytical step for this type of qualitative data.
A frequent criticism of coding method is that it seeks to transform qualitative data into empirically valid data that contain actual value range, structural proportion, contrast ratios, and scientific objective properties. This can tend to drain the data of its variety, richness, and individual character. Analysts respond to this criticism by thoroughly expositing their definitions of codes and linking those codes soundly to the underlying data, therein bringing back some of the richness that might be absent from a mere list of codes.
Alternatives to Coding
Alternatives to coding include recursive abstraction and mechanical techniques. Recursive abstraction involves the summarizing of datasets. Those summaries are then further summarized and so on. The end result is a more compact summary that would have been difficult to accurately discern without the preceding steps of distillation.
Mechanical techniques rely on leveraging computers to scan and reduce large sets of qualitative data. At their most basic level, mechanical techniques rely on counting words, phrases, or coincidences of tokens within the data. Often referred to as content analysis, the output from these techniques is amenable to many advanced statistical analyses.
4.2.2: Interpreting Distributions Constructed by Others
Graphs of distributions created by others can be misleading, either intentionally or unintentionally.
Learning Objective
Demonstrate how distributions constructed by others may be misleading, either intentionally or unintentionally.
Key Points
- Misleading graphs will misrepresent data, constituting a misuse of statistics that may result in an incorrect conclusion being derived from them.
- Graphs can be misleading if they’re used excessively, if they use the third dimensions where it is unnecessary, if they are improperly scaled, or if they’re truncated.
- The use of biased or loaded words in the graph’s title, axis labels, or caption may inappropriately prime the reader.
Key Terms
- bias
-
(Uncountable) Inclination towards something; predisposition, partiality, prejudice, preference, predilection.
- distribution
-
the set of relative likelihoods that a variable will have a value in a given interval
- truncate
-
To shorten something as if by cutting off part of it.
Distributions Constructed by Others
Unless you are constructing a graph of a distribution on your own, you need to be very careful about how you read and interpret graphs. Graphs are made in order to display data; however, some people may intentionally try to mislead the reader in order to convey certain information.
In statistics, these types of graphs are called misleading graphs (or distorted graphs). They misrepresent data, constituting a misuse of statistics that may result in an incorrect conclusion being derived from them. Graphs may be misleading through being excessively complex or poorly constructed. Even when well-constructed to accurately display the characteristics of their data, graphs can be subject to different interpretation.
Misleading graphs may be created intentionally to hinder the proper interpretation of data, but can also be created accidentally by users for a variety of reasons including unfamiliarity with the graphing software, the misinterpretation of the data, or because the data cannot be accurately conveyed. Misleading graphs are often used in false advertising.
Types of Misleading Graphs
The use of graphs where they are not needed can lead to unnecessary confusion/interpretation. Generally, the more explanation a graph needs, the less the graph itself is needed. Graphs do not always convey information better than tables. This is often called excessive usage.
The use of biased or loaded words in the graph’s title, axis labels, or caption may inappropriately prime the reader.
Pie charts can be especially misleading. Comparing pie charts of different sizes could be misleading as people cannot accurately read the comparative area of circles. The usage of thin slices which are hard to discern may be difficult to interpret. The usage of percentages as labels on a pie chart can be misleading when the sample size is small. A perspective (3D) pie chart is used to give the chart a 3D look. Often used for aesthetic reasons, the third dimension does not improve the reading of the data; on the contrary, these plots are difficult to interpret because of the distorted effect of perspective associated with the third dimension. In a 3D pie chart, the slices that are closer to the reader appear to be larger than those in the back due to the angle at which they’re presented .
3-D Pie Chart
In the misleading pie chart, Item C appears to be at least as large as Item A, whereas in actuality, it is less than half as large.
When using pictogram in bar graphs, they should not be scaled uniformly as this creates a perceptually misleading comparison. The area of the pictogram is interpreted instead of only its height or width. This causes the scaling to make the difference appear to be squared .
Improper Scaling
Note how in the improperly scaled pictogram bar graph, the image for B is actually 9 times larger than A.
A truncated graph has a y-axis that does not start at 0. These graphs can create the impression of important change where there is relatively little change .
Truncated Bar Graph
Note that both of these graphs display identical data; however, in the truncated bar graph on the left, the data appear to show significant differences, whereas in the regular bar graph on the right, these differences are hardly visible.
Usage in the Real World
Graphs are useful in the summary and interpretation of financial data. Graphs allow for trends in large data sets to be seen while also allowing the data to be interpreted by non-specialists. Graphs are often used in corporate annual reports as a form of impression management. In the United States, graphs do not have to be audited as they fall under AU Section 550 Other Information in Documents Containing Audited Financial Statements. Several published studies have looked at the usage of graphs in corporate reports for different corporations in different countries and have found frequent usage of improper design, selectivity, and measurement distortion within these reports. The presence of misleading graphs in annual reports have led to requests for standards to be set. Research has found that while readers with poor levels of financial understanding have a greater chance of being misinformed by misleading graphs, even those with financial understanding, such as loan officers, may be misled.
4.2.3: Graphs of Qualitative Data
Qualitative data can be graphed in various ways, including using pie charts and bar charts.
Learning Objective
Create a pie chart and bar chart representing qualitative data.
Key Points
- Since qualitative data represent individual categories, calculating descriptive statistics is limited. Mean, median, and measures of spread cannot be calculated; however, the mode can be calculated.
- One way in which we can graphically represent qualitative data is in a pie chart. Categories are represented by slices of the pie, whose areas are proportional to the percentage of items in that category.
- The key point about the qualitative data is that they do not come with a pre-established ordering (the way numbers are ordered).
- Bar charts can also be used to graph qualitative data. The Y axis displays the frequencies and the X axis displays the categories.
Key Term
- descriptive statistics
-
A branch of mathematics dealing with summarization and description of collections of data sets, including the concepts of arithmetic mean, median, and mode.
Qualitative Data
Recall the difference between quantitative and qualitative data. Quantitative data are data about numeric values. Qualitative data are measures of types and may be represented as a name or symbol. Statistics that describe or summarize can be produced for quantitative data and to a lesser extent for qualitative data. As quantitative data are always numeric they can be ordered, added together, and the frequency of an observation can be counted. Therefore, all descriptive statistics can be calculated using quantitative data. As qualitative data represent individual (mutually exclusive) categories, the descriptive statistics that can be calculated are limited, as many of these techniques require numeric values which can be logically ordered from lowest to highest and which express a count. Mode can be calculated, as it it the most frequency observed value. Median, measures of shape, measures of spread such as the range and interquartile range, require an ordered data set with a logical low-end value and high-end value. Variance and standard deviation require the mean to be calculated, which is not appropriate for categorical variables as they have no numerical value.
Graphing Qualitative Data
There are a number of ways in which qualitative data can be displayed. A good way to demonstrate the different types of graphs is by looking at the following example:
When Apple Computer introduced the iMac computer in August 1998, the company wanted to learn whether the iMac was expanding Apple’s market share. Was the iMac just attracting previous Macintosh owners? Or was it purchased by newcomers to the computer market, and by previous Windows users who were switching over? To find out, 500 iMac customers were interviewed. Each customer was categorized as a previous Macintosh owners, a previous Windows owner, or a new computer purchaser. The qualitative data results were displayed in a frequency table.
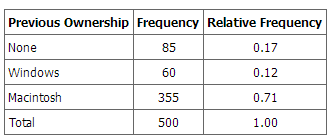
Frequency Table for Mac Data
The frequency table shows how many people in the study were previous Mac owners, previous Windows owners, or neither.
The key point about the qualitative data is that they do not come with a pre-established ordering (the way numbers are ordered). For example, there is no natural sense in which the category of previous Windows users comes before or after the category of previous iMac users. This situation may be contrasted with quantitative data, such as a person’s weight. People of one weight are naturally ordered with respect to people of a different weight.
Pie Charts
One way in which we can graphically represent this qualitative data is in a pie chart. In a pie chart, each category is represented by a slice of the pie. The area of the slice is proportional to the percentage of responses in the category. This is simply the relative frequency multiplied by 100. Although most iMac purchasers were Macintosh owners, Apple was encouraged by the 12% of purchasers who were former Windows users, and by the 17% of purchasers who were buying a computer for the first time .
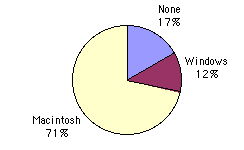
Pie Chart for Mac Data
The pie chart shows how many people in the study were previous Mac owners, previous Windows owners, or neither.
Pie charts are effective for displaying the relative frequencies of a small number of categories. They are not recommended, however, when you have a large number of categories. Pie charts can also be confusing when they are used to compare the outcomes of two different surveys or experiments.
Here is another important point about pie charts. If they are based on a small number of observations, it can be misleading to label the pie slices with percentages. For example, if just 5 people had been interviewed by Apple Computers, and 3 were former Windows users, it would be misleading to display a pie chart with the Windows slice showing 60%. With so few people interviewed, such a large percentage of Windows users might easily have accord since chance can cause large errors with small samples. In this case, it is better to alert the user of the pie chart to the actual numbers involved. The slices should therefore be labeled with the actual frequencies observed (e.g., 3) instead of with percentages.
Bar Charts
Bar charts can also be used to represent frequencies of different categories . Frequencies are shown on the Y axis and the type of computer previously owned is shown on the X axis. Typically the Y-axis shows the number of observations rather than the percentage of observations in each category as is typical in pie charts.
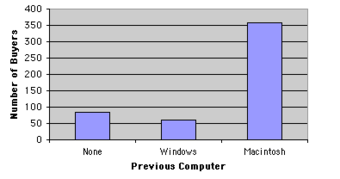
Bar Chart for Mac Data
The bar chart shows how many people in the study were previous Mac owners, previous Windows owners, or neither.
4.2.4: Misleading Graphs
A misleading graph misrepresents data and may result in incorrectly derived conclusions.
Learning Objective
Criticize the practices of excessive usage, biased labeling, improper scaling, truncating, and the addition of a third dimension that often result in misleading graphs.
Key Points
- Misleading graphs may be created intentionally to hinder the proper interpretation of data, but can be also created accidentally by users for a variety of reasons.
- The use of graphs where they are not needed can lead to unnecessary confusion/interpretation. This is referred to as excessive usage.
- The use of biased or loaded words in the graph’s title, axis labels, or caption may inappropriately sway the reader. This is called biased labeling.
- Graphs can also be misleading if they are improperly labeled, if they are truncated, if there is an axis change, if they lack a scale, or if they are unnecessarily displayed in the third dimension.
Key Terms
- pictogram
-
a picture that represents a word or an idea by illustration; used often in graphs
- volatility
-
the state of sharp and regular fluctuation
What is a Misleading Graph?
In statistics, a misleading graph, also known as a distorted graph, is a graph which misrepresents data, constituting a misuse of statistics and with the result that an incorrect conclusion may be derived from it. Graphs may be misleading through being excessively complex or poorly constructed. Even when well-constructed to accurately display the characteristics of their data, graphs can be subject to different interpretation.
Misleading graphs may be created intentionally to hinder the proper interpretation of data, but can be also created accidentally by users for a variety of reasons including unfamiliarity with the graphing software, the misinterpretation of the data, or because the data cannot be accurately conveyed. Misleading graphs are often used in false advertising. One of the first authors to write about misleading graphs was Darrell Huff, who published the best-selling book How to Lie With Statistics in 1954. It is still in print.
Excessive Usage
There are numerous ways in which a misleading graph may be constructed. The use of graphs where they are not needed can lead to unnecessary confusion/interpretation. Generally, the more explanation a graph needs, the less the graph itself is needed. Graphs do not always convey information better than tables.
Biased Labeling
The use of biased or loaded words in the graph’s title, axis labels, or caption may inappropriately sway the reader.
Improper Scaling
When using pictogram in bar graphs, they should not be scaled uniformly as this creates a perceptually misleading comparison. The area of the pictogram is interpreted instead of only its height or width. This causes the scaling to make the difference appear to be squared.
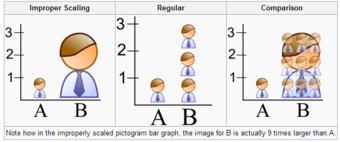
Improper Scaling
In the improperly scaled pictogram bar graph, the image for B is actually 9 times larger than A.
Truncated Graphs
A truncated graph has a y-axis that does not start at zero. These graphs can create the impression of important change where there is relatively little change.Truncated graphs are useful in illustrating small differences. Graphs may also be truncated to save space. Commercial software such as MS Excel will tend to truncate graphs by default if the values are all within a narrow range.
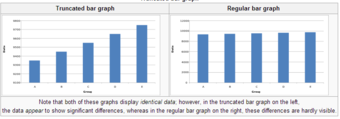
Truncated Bar Graph
Both of these graphs display identical data; however, in the truncated bar graph on the left, the data appear to show significant differences, whereas in the regular bar graph on the right, these differences are hardly visible.
Misleading 3D Pie Charts
A perspective (3D) pie chart is used to give the chart a 3D look. Often used for aesthetic reasons, the third dimension does not improve the reading of the data; on the contrary, these plots are difficult to interpret because of the distorted effect of perspective associated with the third dimension. The use of superfluous dimensions not used to display the data of interest is discouraged for charts in general, not only for pie charts. In a 3D pie chart, the slices that are closer to the reader appear to be larger than those in the back due to the angle at which they’re presented .
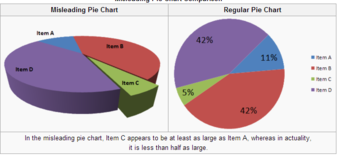
Misleading 3D Pie Chart
In the misleading pie chart, Item C appears to be at least as large as Item A, whereas in actuality, it is less than half as large.
Other Misleading Graphs
Graphs can also be misleading for a variety of other reasons. An axis change affects how the graph appears in terms of its growth and volatility. A graph with no scale can be easily manipulated to make the difference between bars look larger or smaller than they actually are. Improper intervals can affect the appearance of a graph, as well as omitting data. Finally, graphs can also be misleading if they are overly complex or poorly constructed.
Graphs in Finance and Corporate Reports
Graphs are useful in the summary and interpretation of financial data. Graphs allow for trends in large data sets to be seen while also allowing the data to be interpreted by non-specialists. Graphs are often used in corporate annual reports as a form of impression management. In the United States, graphs do not have to be audited. Several published studies have looked at the usage of graphs in corporate reports for different corporations in different countries and have found frequent usage of improper design, selectivity, and measurement distortion within these reports. The presence of misleading graphs in annual reports have led to requests for standards to be set. Research has found that while readers with poor levels of financial understanding have a greater chance of being misinformed by misleading graphs, even those with financial understanding, such as loan officers, may be misled.
4.2.5: Do It Yourself: Plotting Qualitative Frequency Distributions
Qualitative frequency distributions can be displayed in bar charts, Pareto charts, and pie charts.
Learning Objective
Outline the steps necessary to plot a frequency distribution for qualitative data.
Key Points
- The first step to plotting a qualitative frequency distributions is to create a frequency table.
- If drawing a bar graph or Pareto chart, first draw two axes. The y-axis is labeled with the frequency (or relative frequency) and the x-axis is labeled with the category.
- In bar graphs and Pareto graphs, draw rectangles of equal width and heights that correspond to their frequencies/relative frequencies.
- A pie chart shows the distribution in a different way, where each percentage is a slice of the pie.
Key Terms
- relative frequency distribution
-
a representation, either in graphical or tabular format, which displays the fraction of observations in a certain category
- frequency distribution
-
a representation, either in a graphical or tabular format, which displays the number of observations within a given interval
- Pareto chart
-
a type of bar graph where where the bars are drawn in decreasing order of frequency or relative frequency
Ways to Organize Data
When data is collected from a survey or an experiment, they must be organized into a manageable form. Data that is not organized is referred to as raw data. A few different ways to organize data include tables, graphs, and numerical summaries.
One common way to organize qualitative, or categorical, data is in a frequency distribution. A frequency distribution lists the number of occurrences for each category of data.
Step-by-Step Guide to Plotting Qualitative Frequency Distributions
The first step towards plotting a qualitative frequency distribution is to create a table of the given or collected data. For example, let’s say you want to determine the distribution of colors in a bag of Skittles. You open up a bag, and you find that there are 15 red, 7 orange, 7 yellow, 13 green, and 8 purple. Create a two column chart, with the titles of Color and Frequency, and fill in the corresponding data.
To construct a frequency distribution in the form of a bar graph, you must first draw two axes. The y-axis (vertical axis) should be labeled with the frequencies and the x-axis (horizontal axis) should be labeled with each category (in this case, Skittle color). The graph is completed by drawing rectangles of equal width for each color, each as tall as their frequency .
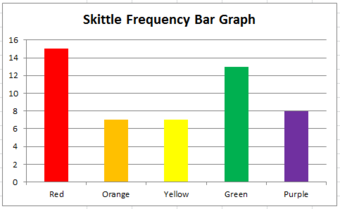
Bar Graph
This graph shows the frequency distribution of a bag of Skittles.
Sometimes a relative frequency distribution is desired. If this is the case, simply add a third column in the table called Relative Frequency. This is found by dividing the frequency of each color by the total number of Skittles (50, in this case). This number can be written as a decimal, a percentage, or as a fraction. If we decided to use decimals, the relative frequencies for the red, orange, yellow, green, and purple Skittles are respectively 0.3, 0.14, 0.14, 0.26, and 0.16. The decimals should add up to 1 (or very close to it due to rounding). Bar graphs for relative frequency distributions are very similar to bar graphs for regular frequency distributions, except this time, the y-axis will be labeled with the relative frequency rather than just simply the frequency. A special type of bar graph where the bars are drawn in decreasing order of relative frequency is called a Pareto chart .
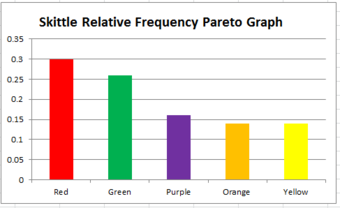
Pareto Chart
This graph shows the relative frequency distribution of a bag of Skittles.
The distribution can also be displayed in a pie chart, where the percentages of the colors are broken down into slices of the pie. This may be done by hand, or by using a computer program such as Microsoft Excel . If done by hand, you must find out how many degrees each piece of the pie corresponds to. Since a circle has 360 degrees, this is found out by multiplying the relative frequencies by 360. The respective degrees for red, orange, yellow, green, and purple in this case are 108, 50.4, 50.4, 93.6, and 57.6. Then, use a protractor to properly draw in each slice of the pie.
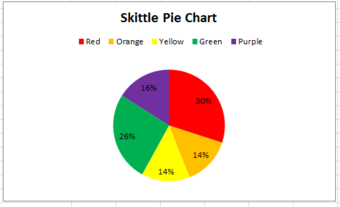
Pie Chart
This pie chart shows the frequency distribution of a bag of Skittles.
4.2.6: Summation Notation
In statistical formulas that involve summing numbers, the Greek letter sigma is used as the summation notation.
Learning Objective
Discuss the summation notation and identify statistical situations in which it may be useful or even essential.
Key Points
- There is no special notation for the summation of explicit sequences (such as
), as the corresponding repeated addition expression will do. - If the terms of the sequence are given by a regular pattern, possibly of variable length, then the summation notation may be useful or even essential.
- In general, mathematicians use the following sigma notation:
, where
is the lower bound,
is the upper bound,
is the index of summation, and
represents each successive term to be added.
Key Terms
- summation notation
-
a notation, given by the Greek letter sigma, that denotes the operation of adding a sequence of numbers
- ellipsis
-
a mark consisting of three periods, historically with spaces in between, before, and after them ” . . . “, nowadays a single character ” (used in printing to indicate an omission)
Summation
Many statistical formulas involve summing numbers. Fortunately there is a convenient notation for expressing summation. This section covers the basics of this summation notation.
Summation is the operation of adding a sequence of numbers, the result being their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed (called addends, or sometimes summands) may be integers, rational numbers, real numbers, or complex numbers. Besides numbers, other types of values can be added as well: vectors, matrices, polynomials and, in general, elements of any additive group. For finite sequences of such elements, summation always produces a well-defined sum.
The summation of the sequence
is an expression whose value is the sum of each of the members of the sequence. In the example,
. Since addition is associative, the value does not depend on how the additions are grouped. For instance
and
both have the value
; therefore, parentheses are usually omitted in repeated additions. Addition is also commutative, so changing the order of the terms of a finite sequence does not change its sum.
Notation
There is no special notation for the summation of such explicit sequences as the example above, as the corresponding repeated addition expression will do. If, however, the terms of the sequence are given by a regular pattern, possibly of variable length, then a summation operator may be useful or even essential.
For the summation of the sequence of consecutive integers from 1 to 100 one could use an addition expression involving an ellipsis to indicate the missing terms:
. In this case the reader easily guesses the pattern; however, for more complicated patterns, one needs to be precise about the rule used to find successive terms. This can be achieved by using the summation notation “
” Using this sigma notation, the above summation is written as:
In general, mathematicians use the following sigma notation:
In this notation,
represents the index of summation,
is an indexed variable representing each successive term in the series,
is the lower bound of summation, and
is the upper bound of summation. The “
” under the summation symbol means that the index
starts out equal to
. The index,
, is incremented by 1 for each successive term, stopping when
.
Here is an example showing the summation of exponential terms (terms to the power of 2):
Informal writing sometimes omits the definition of the index and bounds of summation when these are clear from context, as in:
One often sees generalizations of this notation in which an arbitrary logical condition is supplied, and the sum is intended to be taken over all values satisfying the condition. For example, the sum of
over all integers
in the specified range can be written as:
The sum of
over all elements
in the set
can be written as:
4.2.7: Graphing Bivariate Relationships
We can learn much more by displaying bivariate data in a graphical form that maintains the pairing of variables.
Learning Objective
Compare the strengths and weaknesses of the various methods used to graph bivariate data.
Key Points
- When one variable increases with the second variable, we say that x and y have a positive association.
- Conversely, when y decreases as x increases, we say that they have a negative association.
- The presence of qualitative data leads to challenges in graphing bivariate relationships.
- If both variables are qualitative, we would be able to graph them in a contingency table.
Key Terms
- bivariate
-
Having or involving exactly two variables.
- contingency table
-
a table presenting the joint distribution of two categorical variables
- skewed
-
Biased or distorted (pertaining to statistics or information).
Introduction to Bivariate Data
Measures of central tendency, variability, and spread summarize a single variable by providing important information about its distribution. Often, more than one variable is collected on each individual. For example, in large health studies of populations it is common to obtain variables such as age, sex, height, weight, blood pressure, and total cholesterol on each individual. Economic studies may be interested in, among other things, personal income and years of education. As a third example, most university admissions committees ask for an applicant’s high school grade point average and standardized admission test scores (e.g., SAT). In the following text, we consider bivariate data, which for now consists of two quantitative variables for each individual. Our first interest is in summarizing such data in a way that is analogous to summarizing univariate (single variable) data.
By way of illustration, let’s consider something with which we are all familiar: age. More specifically, let’s consider if people tend to marry other people of about the same age. One way to address the question is to look at pairs of ages for a sample of married couples. Bivariate Sample 1 shows the ages of 10 married couples. Going across the columns we see that husbands and wives tend to be of about the same age, with men having a tendency to be slightly older than their wives.

Bivariate Sample 1
Sample of spousal ages of 10 white American couples.
These pairs are from a dataset consisting of 282 pairs of spousal ages (too many to make sense of from a table). What we need is a way to graphically summarize the 282 pairs of ages, such as a histogram. as in .
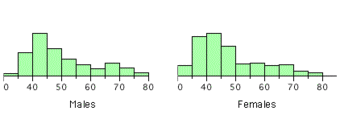
Bivariate Histogram
Histogram of spousal ages.
Each distribution is fairly skewed with a long right tail. From the first figure we see that not all husbands are older than their wives. It is important to see that this fact is lost when we separate the variables. That is, even though we provide summary statistics on each variable, the pairing within couples is lost by separating the variables. Only by maintaining the pairing can meaningful answers be found about couples, per se.
Therefore, we can learn much more by displaying the bivariate data in a graphical form that maintains the pairing. shows a scatter plot of the paired ages. The x-axis represents the age of the husband and the y-axis the age of the wife.
Bivariate Scatterplot
Scatterplot showing wife age as a function of husband age.
There are two important characteristics of the data revealed by this figure. First, it is clear that there is a strong relationship between the husband’s age and the wife’s age: the older the husband, the older the wife. When one variable increases with the second variable, we say that x and y have a positive association. Conversely, when y decreases as x increases, we say that they have a negative association. Second, the points cluster along a straight line. When this occurs, the relationship is called a linear relationship.
Bivariate Relationships in Qualitative Data
The presence of qualitative data leads to challenges in graphing bivariate relationships. We could have one qualitative variable and one quantitative variable, such as SAT subject and score. However, making a scatter plot would not be possible as only one variable is numerical. A bar graph would be possible.
If both variables are qualitative, we would be able to graph them in a contingency table. We can then use this to find whatever information we may want. In , this could include what percentage of the group are female and right-handed or what percentage of the males are left-handed.
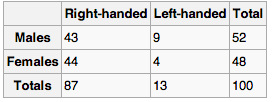
Contingency Table
Contingency tables are useful for graphically representing qualitative bivariate relationships.
Chapter 3: Visualizing Data
3.1: The Histogram
3.1.1: Cross Tabulation
Cross tabulation (or crosstabs for short) is a statistical process that summarizes categorical data to create a contingency table.
Learning Objective
Demonstrate how cross tabulation provides a basic picture of the interrelation between two variables and helps to find interactions between them.
Key Points
- Crosstabs are heavily used in survey research, business intelligence, engineering, and scientific research.
- Crosstabs provide a basic picture of the interrelation between two variables and can help find interactions between them.
- Most general-purpose statistical software programs are able to produce simple crosstabs.
Key Term
- cross tabulation
-
a presentation of data in a tabular form to aid in identifying a relationship between variables
Cross tabulation (or crosstabs for short) is a statistical process that summarizes categorical data to create a contingency table. It is used heavily in survey research, business intelligence, engineering, and scientific research. Moreover, it provides a basic picture of the interrelation between two variables and can help find interactions between them.
In survey research (e.g., polling, market research), a “crosstab” is any table showing summary statistics. Commonly, crosstabs in survey research are combinations of multiple different tables. For example, combines multiple contingency tables and tables of averages.
Crosstab of Cola Preference by Age and Gender
A crosstab is a combination of various tables showing summary statistics.
Contingency Tables
A contingency table is a type of table in a matrix format that displays the (multivariate) frequency distribution of the variables. A crucial problem of multivariate statistics is finding the direct dependence structure underlying the variables contained in high dimensional contingency tables. If some of the conditional independences are revealed, then even the storage of the data can be done in a smarter way. In order to do this, one can use information theory concepts, which gain the information only from the distribution of probability. Probability can be expressed easily from the contingency table by the relative frequencies.
As an example, suppose that we have two variables, sex (male or female) and handedness (right- or left-handed). Further suppose that 100 individuals are randomly sampled from a very large population as part of a study of sex differences in handedness. A contingency table can be created to display the numbers of individuals who are male and right-handed, male and left-handed, female and right-handed, and female and left-handed .
Contingency Table
Contingency table created to display the numbers of individuals who are male and right-handed, male and left-handed, female and right-handed, and female and left-handed.
The numbers of the males, females, and right-and-left-handed individuals are called marginal totals. The grand total–i.e., the total number of individuals represented in the contingency table– is the number in the bottom right corner.
The table allows us to see at a glance that the proportion of men who are right-handed is about the same as the proportion of women who are right-handed, although the proportions are not identical. If the proportions of individuals in the different columns vary significantly between rows (or vice versa), we say that there is a contingency between the two variables. In other words, the two variables are not independent. If there is no contingency, we say that the two variables are independent.
Standard Components of a Crosstab
- Multiple columns – each column refers to a specific sub-group in the population (e.g., men). The columns are sometimes referred to as banner points or cuts (and the rows are sometimes referred to as stubs).
- Significance tests – typically, either column comparisons–which test for differences between columns and display these results using letters– or cell comparisons–which use color or arrows to identify a cell in a table that stands out in some way (as in the example above).
- Nets or netts – which are sub-totals.
- One or more of the following: percentages, row percentages, column percentages, indexes, or averages.
- Unweighted sample sizes (i.e., counts).
Most general-purpose statistical software programs are able to produce simple crosstabs. Creation of the standard crosstabs used in survey research, as shown above, is typically done using specialist crosstab software packages, such as:
- New Age Media Systems (EzTab)
- SAS
- Quantum
- Quanvert
- SPSS Custom Tables
- IBM SPSS Data Collection Model programs
- Uncle
- WinCross
- Q
- SurveyCraft
- BIRT
3.1.2: Drawing a Histogram
To draw a histogram, one must decide how many intervals represent the data, the width of the intervals, and the starting point for the first interval.
Learning Objective
Outline the steps involved in creating a histogram.
Key Points
- There is no “best” number of bars, and different bar sizes may reveal different features of the data.
- A convenient starting point for the first interval is a lower value carried out to one more decimal place than the value with the most decimal places.
- To calculate the width of the intervals, subtract the starting point from the ending value and divide by the number of bars.
Key Term
- histogram
-
a representation of tabulated frequencies, shown as adjacent rectangles, erected over discrete intervals (bins), with an area equal to the frequency of the observations in the interval
To construct a histogram, one must first decide how many bars or intervals (also called classes) are needed to represent the data. Many histograms consist of between 5 and 15 bars, or classes. One must choose a starting point for the first interval, which must be less than the smallest data value. A convenient starting point is a lower value carried out to one more decimal place than the value with the most decimal places.
For example, if the value with the most decimal places is 6.1, and this is the smallest value, a convenient starting point is 6.05 (
). We say that 6.05 has more precision. If the value with the most decimal places is 2.23 and the lowest value is 1.5, a convenient starting point is 1.495 (
). If the value with the most decimal places is 3.234 and the lowest value is 1.0, a convenient starting point is 0.9995 (
). If all the data happen to be integers and the smallest value is 2, then a convenient starting point is 1.5 (
). Also, when the starting point and other boundaries are carried to one additional decimal place, no data value will fall on a boundary.
Consider the following data, which are the heights (in inches to the nearest half inch) of 100 male semiprofessional soccer players. The heights are continuous data since height is measured.
60; 60.5; 61; 61; 61.5; 63.5; 63.5; 63.5; 64; 64; 64; 64; 64; 64; 64; 64.5; 64.5; 64.5; 64.5; 64.5; 64.5; 64.5; 64.5; 66; 66; 66; 66; 66; 66; 66; 66; 66; 66; 66.5; 66.5; 66.5; 66.5; 66.5; 66.5; 66.5; 66.5; 66.5; 66.5; 66.5; 67; 67; 67; 67; 67; 67; 67; 67; 67; 67; 67; 67; 67.5; 67.5; 67.5; 67.5; 67.5; 67.5; 67.5; 68; 68; 69; 69; 69; 69; 69; 69; 69; 69; 69; 69; 69.5; 69.5; 69.5; 69.5; 69.5; 70; 70; 70; 70; 70; 70; 70.5; 70.5; 70.5; 71; 71; 71; 72; 72; 72; 72.5; 72.5; 73; 73.5; 74
The smallest data value is 60. Since the data with the most decimal places has one decimal (for instance, 61.5), we want our starting point to have two decimal places. Since the numbers 0.5, 0.05, 0.005, and so on are convenient numbers, use 0.05 and subtract it from 60, the smallest value, for the convenient starting point. The starting point, then, is 59.95.
The largest value is 74.
is the ending value.
Next, calculate the width of each bar or class interval. To calculate this width, subtract the starting point from the ending value and divide by the number of bars (you must choose the number of bars you desire). Note that there is no “best” number of bars, and different bar sizes can reveal different features of the data. Some theoreticians have attempted to determine an optimal number of bars, but these methods generally make strong assumptions about the shape of the distribution. Depending on the actual data distribution and the goals of the analysis, different bar widths may be appropriate, so experimentation is usually needed to determine an appropriate width.
Suppose, in our example, we choose 8 bars. The bar width will be as follows:
We will round up to 2 and make each bar or class interval 2 units wide. Rounding up to 2 is one way to prevent a value from falling on a boundary. The boundaries are:
59.95, 61.95, 63.95, 65.95, 67.95, 69.95, 71.95, 73.95, 75.95
So that there are 2 units between each boundary.
The heights 60 through 61.5 inches are in the interval 59.95 – 61.95. The heights that are 63.5 are in the interval 61.95 – 63.95. The heights that are 64 through 64.5 are in the interval 63.95 – 65.95. The heights 66 through 67.5 are in the interval 65.95 – 67.95. The heights 68 through 69.5 are in the interval 67.95 – 69.95. The heights 70 through 71 are in the interval 69.95 – 71.95. The heights 72 through 73.5 are in the interval 71.95 – 73.95. The height 74 is in the interval 73.95 – 75.95.
displays the heights on the x-axis and relative frequency on the y-axis.
Histogram Example
This histogram depicts the relative frequency of heights for 100 semiprofessional soccer players. Note the roughly normal distribution, with the center of the curve around 66 inches.
3.1.3: Recognizing and Using a Histogram
A histogram is a graphical representation of the distribution of data.
Learning Objective
Indicate how frequency and probability distributions are represented by histograms.
Key Points
- First introduced by Karl Pearson, a histogram is an estimate of the probability distribution of a continuous variable.
- If the distribution of
is continuous, then
is called a continuous random variable and, therefore, has a continuous probability distribution. - An advantage of a histogram is that it can readily display large data sets (a rule of thumb is to use a histogram when the data set consists of 100 values or more).
Key Terms
- frequency
-
number of times an event occurred in an experiment (absolute frequency)
- histogram
-
a representation of tabulated frequencies, shown as adjacent rectangles, erected over discrete intervals (bins), with an area equal to the frequency of the observations in the interval
- probability distribution
-
A function of a discrete random variable yielding the probability that the variable will have a given value.
A histogram is a graphical representation of the distribution of data. More specifically, a histogram is a representation of tabulated frequencies, shown as adjacent rectangles, erected over discrete intervals (bins), with an area equal to the frequency of the observations in the interval. First introduced by Karl Pearson, it is an estimate of the probability distribution of a continuous variable.
A histogram has both a horizontal axis and a vertical axis. The horizontal axis is labeled with what the data represents (for instance, distance from your home to school). The vertical axis is labeled either frequency or relative frequency. The graph will have the same shape with either label. An advantage of a histogram is that it can readily display large data sets (a rule of thumb is to use a histogram when the data set consists of 100 values or more). The histogram can also give you the shape, the center, and the spread of the data.
The categories of a histogram are usually specified as consecutive, non-overlapping intervals of a variable. The categories (intervals) must be adjacent and often are chosen to be of the same size. The rectangles of a histogram are drawn so that they touch each other to indicate that the original variable is continuous.
Frequency and Probability Distributions
In statistical terms, the frequency of an event is the number of times the event occurred in an experiment or study. The relative frequency (or empirical probability) of an event refers to the absolute frequency normalized by the total number of events:
Put more simply, the relative frequency is equal to the frequency for an observed value of the data divided by the total number of data values in the sample.
The height of a rectangle in a histogram is equal to the frequency density of the interval, i.e., the frequency divided by the width of the interval. A histogram may also be normalized displaying relative frequencies. It then shows the proportion of cases that fall into each of several categories, with the total area equaling one.
As mentioned, a histogram is an estimate of the probability distribution of a continuous variable. To define probability distributions for the simplest cases, one needs to distinguish between discrete and continuous random variables. In the discrete case, one can easily assign a probability to each possible value. For example, when throwing a die, each of the six values 1 to 6 has the probability 1/6. In contrast, when a random variable takes values from a continuum, probabilities are nonzero only if they refer to finite intervals. For example, in quality control one might demand that the probability of a “500 g” package containing between 490 g and 510 g should be no less than 98%.
Intuitively, a continuous random variable is the one which can take a continuous range of values — as opposed to a discrete distribution, where the set of possible values for the random variable is, at most, countable. If the distribution of
is continuous, then
is called a continuous random variable and, therefore, has a continuous probability distribution. There are many examples of continuous probability distributions: normal, uniform, chi-squared, and others.

The Histogram
This is an example of a histogram, depicting graphically the distribution of heights for 31 Black Cherry trees.
3.1.4: The Density Scale
Density estimation is the construction of an estimate based on observed data of an unobservable, underlying probability density function.
Learning Objective
Describe how density estimation is used as a tool in the construction of a histogram.
Key Points
- The unobservable density function is thought of as the density according to which a large population is distributed. The data are usually thought of as a random sample from that population.
- A probability density function, or density of a continuous random variable, is a function that describes the relative likelihood for a random variable to take on a given value.
- Kernel density estimates are closely related to histograms, but can be endowed with properties such as smoothness or continuity by using a suitable kernel.
Key Terms
- quartile
-
any of the three points that divide an ordered distribution into four parts, each containing a quarter of the population
- density
-
the probability that an event will occur, as a function of some observed variable
- interquartile range
-
The difference between the first and third quartiles; a robust measure of sample dispersion.
Density Estimation
Histograms are used to plot the density of data, and are often a useful tool for density estimation. Density estimation is the construction of an estimate based on observed data of an unobservable, underlying probability density function. The unobservable density function is thought of as the density according to which a large population is distributed. The data are usually thought of as a random sample from that population.
A probability density function, or density of a continuous random variable, is a function that describes the relative likelihood for this random variable to take on a given value. The probability for the random variable to fall within a particular region is given by the integral of this variable’s density over the region .

Boxplot Versus Probability Density Function
This image shows a boxplot and probability density function of a normal distribution.
The above image depicts a probability density function graph against a box plot. A box plot is a convenient way of graphically depicting groups of numerical data through their quartiles. The spacings between the different parts of the box help indicate the degree of dispersion (spread) and skewness in the data and to identify outliers. In addition to the points themselves, box plots allow one to visually estimate the interquartile range.
A range of data clustering techniques are used as approaches to density estimation, with the most basic form being a rescaled histogram.
Kernel Density Estimation
Kernel density estimates are closely related to histograms, but can be endowed with properties such as smoothness or continuity by using a suitable kernel. To see this, we compare the construction of histogram and kernel density estimators using these 6 data points:
,
,
,
,
,
For the histogram, first the horizontal axis is divided into sub-intervals, or bins, which cover the range of the data. In this case, we have 6 bins, each having a width of 2. Whenever a data point falls inside this interval, we place a box of height
. If more than one data point falls inside the same bin, we stack the boxes on top of each other .
Histogram Versus Kernel Density Estimation
Comparison of the histogram (left) and kernel density estimate (right) constructed using the same data. The 6 individual kernels are the red dashed curves, the kernel density estimate the blue curves. The data points are the rug plot on the horizontal axis.
For the kernel density estimate, we place a normal kernel with variance 2.25 (indicated by the red dashed lines) on each of the data points
. The kernels are summed to make the kernel density estimate (the solid blue curve). Kernel density estimates converge faster to the true underlying density for continuous random variables thus accounting for their smoothness compared to the discreteness of the histogram.
3.1.5: Types of Variables
A variable is any characteristic, number, or quantity that can be measured or counted.
Learning Objective
Distinguish between quantitative and categorical, continuous and discrete, and ordinal and nominal variables.
Key Points
- Numeric (quantitative) variables have values that describe a measurable quantity as a number, like “how many” or “how much”.
- A continuous variable is an observation that can take any value between a certain set of real numbers.
- A discrete variable is an observation that can take a value based on a count from a set of distinct whole values.
- Categorical variables have values that describe a “quality” or “characteristic” of a data unit, like “what type” or “which category”.
- An ordinal variable is an observation that can take a value that can be logically ordered or ranked.
- A nominal variable is an observation that can take a value that is not able to be organized in a logical sequence.
Key Terms
- continuous variable
-
a variable that has a continuous distribution function, such as temperature
- discrete variable
-
a variable that takes values from a finite or countable set, such as the number of legs of an animal
- variable
-
a quantity that may assume any one of a set of values
What Is a Variable?
A variable is any characteristic, number, or quantity that can be measured or counted. A variable may also be called a data item. Age, sex, business income and expenses, country of birth, capital expenditure, class grades, eye colour and vehicle type are examples of variables. Variables are so-named because their value may vary between data units in a population and may change in value over time.
What Are the Types of Variables?
There are different ways variables can be described according to the ways they can be studied, measured, and presented. Numeric variables have values that describe a measurable quantity as a number, like “how many” or “how much. ” Therefore, numeric variables are quantitative variables.
Numeric variables may be further described as either continuous or discrete. A continuous variable is a numeric variable. Observations can take any value between a certain set of real numbers. The value given to an observation for a continuous variable can include values as small as the instrument of measurement allows. Examples of continuous variables include height, time, age, and temperature.
A discrete variable is a numeric variable. Observations can take a value based on a count from a set of distinct whole values. A discrete variable cannot take the value of a fraction between one value and the next closest value. Examples of discrete variables include the number of registered cars, number of business locations, and number of children in a family, all of of which measured as whole units (i.e., 1, 2, 3 cars).
Categorical variables have values that describe a “quality” or “characteristic” of a data unit, like “what type” or “which category. ” Categorical variables fall into mutually exclusive (in one category or in another) and exhaustive (include all possible options) categories. Therefore, categorical variables are qualitative variables and tend to be represented by a non-numeric value.
Categorical variables may be further described as ordinal or nominal. An ordinal variable is a categorical variable. Observations can take a value that can be logically ordered or ranked. The categories associated with ordinal variables can be ranked higher or lower than another, but do not necessarily establish a numeric difference between each category. Examples of ordinal categorical variables include academic grades (i.e., A, B, C), clothing size (i.e., small, medium, large, extra large) and attitudes (i.e., strongly agree, agree, disagree, strongly disagree).
A nominal variable is a categorical variable. Observations can take a value that is not able to be organized in a logical sequence. Examples of nominal categorical variables include sex, business type, eye colour, religion and brand.
Types of Variables
Variables can be numeric or categorial, being further broken down in continuous and discrete, and nominal and ordinal variables.
3.1.6: Controlling for a Variable
Controlling for a variable is a method to reduce the effect of extraneous variations that may also affect the value of the dependent variable.
Learning Objective
Discuss how controlling for a variable leads to more reliable visualizations of probability distributions.
Key Points
- Variables refer to measurable attributes, as these typically vary over time or between individuals.
- Temperature is an example of a continuous variable, while the number of legs of an animal is an example of a discrete variable.
- In causal models, a distinction is made between “independent variables” and “dependent variables,” the latter being expected to vary in value in response to changes in the former.
- While independent variables can refer to quantities and qualities that are under experimental control, they can also include extraneous factors that influence results in a confusing or undesired manner.
- The essence of controlling is to ensure that comparisons between the control group and the experimental group are only made for groups or subgroups for which the variable to be controlled has the same statistical distribution.
Key Terms
- correlation
-
One of the several measures of the linear statistical relationship between two random variables, indicating both the strength and direction of the relationship.
- control
-
a separate group or subject in an experiment against which the results are compared where the primary variable is low or nonexistence
- variable
-
a quantity that may assume any one of a set of values
Histograms help us to visualize the distribution of data and estimate the probability distribution of a continuous variable. In order for us to create reliable visualizations of these distributions, we must be able to procure reliable results for the data during experimentation. A method that significantly contributes to our success in this matter is the controlling of variables.
Defining Variables
In statistics, variables refer to measurable attributes, as these typically vary over time or between individuals. Variables can be discrete (taking values from a finite or countable set), continuous (having a continuous distribution function), or neither. For instance, temperature is a continuous variable, while the number of legs of an animal is a discrete variable.
In causal models, a distinction is made between “independent variables” and “dependent variables,” the latter being expected to vary in value in response to changes in the former. In other words, an independent variable is presumed to potentially affect a dependent one. In experiments, independent variables include factors that can be altered or chosen by the researcher independent of other factors.
There are also quasi-independent variables, which are used by researchers to group things without affecting the variable itself. For example, to separate people into groups by their sex does not change whether they are male or female. Also, a researcher may separate people, arbitrarily, on the amount of coffee they drank before beginning an experiment.
While independent variables can refer to quantities and qualities that are under experimental control, they can also include extraneous factors that influence results in a confusing or undesired manner. In statistics the technique to work this out is called correlation.
Controlling Variables
In a scientific experiment measuring the effect of one or more independent variables on a dependent variable, controlling for a variable is a method of reducing the confounding effect of variations in a third variable that may also affect the value of the dependent variable. For example, in an experiment to determine the effect of nutrition (the independent variable) on organism growth (the dependent variable), the age of the organism (the third variable) needs to be controlled for, since the effect may also depend on the age of an individual organism.
The essence of the method is to ensure that comparisons between the control group and the experimental group are only made for groups or subgroups for which the variable to be controlled has the same statistical distribution. A common way to achieve this is to partition the groups into subgroups whose members have (nearly) the same value for the controlled variable.
Controlling for a variable is also a term used in statistical data analysis when inferences may need to be made for the relationships within one set of variables, given that some of these relationships may spuriously reflect relationships to variables in another set. This is broadly equivalent to conditioning on the variables in the second set. Such analyses may be described as “controlling for variable
” or “controlling for the variations in
“. Controlling, in this sense, is performed by including in the experiment not only the explanatory variables of interest but also the extraneous variables. The failure to do so results in omitted-variable bias.

Controlling for Variables
Controlling is very important in experimentation to ensure reliable results. For example, in an experiment to see which type of vinegar displays the greatest reaction to baking soda, the brand of baking soda should be controlled.
3.1.7: Selective Breeding
Selective breeding is a field concerned with testing hypotheses and theories of evolution by using controlled experiments.
Learning Objective
Illustrate how controlled experiments have allowed human beings to selectively breed domesticated plants and animals.
Key Points
- Unwittingly, humans have carried out evolution experiments for as long as they have been domesticating plants and animals.
- More recently, evolutionary biologists have realized that the key to successful experimentation lies in extensive parallel replication of evolving lineages as well as a larger number of generations of selection.
- Because of the large number of generations required for adaptation to occur, evolution experiments are typically carried out with microorganisms such as bacteria, yeast, or viruses.
Key Terms
- breeding
-
the process through which propagation, growth, or development occurs
- evolution
-
a gradual directional change, especially one leading to a more advanced or complex form; growth; development
- stochastic
-
random; randomly determined
Experimental Evolution and Selective Breeding
Experimental evolution is a field in evolutionary and experimental biology that is concerned with testing hypotheses and theories of evolution by using controlled experiments. Evolution may be observed in the laboratory as populations adapt to new environmental conditions and/or change by such stochastic processes as random genetic drift.
With modern molecular tools, it is possible to pinpoint the mutations that selection acts upon, what brought about the adaptations, and to find out how exactly these mutations work. Because of the large number of generations required for adaptation to occur, evolution experiments are typically carried out with microorganisms such as bacteria, yeast, or viruses.
History of Selective Breeding
Unwittingly, humans have carried out evolution experiments for as long as they have been domesticating plants and animals. Selective breeding of plants and animals has led to varieties that differ dramatically from their original wild-type ancestors. Examples are the cabbage varieties, maize, or the large number of different dog breeds .

Selective Breeding
This Chihuahua mix and Great Dane show the wide range of dog breed sizes created using artificial selection, or selective breeding.
One of the first to carry out a controlled evolution experiment was William Dallinger. In the late 19th century, he cultivated small unicellular organisms in a custom-built incubator over a time period of seven years (1880–1886). Dallinger slowly increased the temperature of the incubator from an initial 60 °F up to 158 °F. The early cultures had shown clear signs of distress at a temperature of 73 °F, and were certainly not capable of surviving at 158 °F. The organisms Dallinger had in his incubator at the end of the experiment, on the other hand, were perfectly fine at 158 °F. However, these organisms would no longer grow at the initial 60 °F. Dallinger concluded that he had found evidence for Darwinian adaptation in his incubator, and that the organisms had adapted to live in a high-temperature environment .

Dallinger Incubator
Drawing of the incubator used by Dallinger in his evolution experiments.
More recently, evolutionary biologists have realized that the key to successful experimentation lies in extensive parallel replication of evolving lineages as well as a larger number of generations of selection. For example, on February 15, 1988, Richard Lenski started a long-term evolution experiment with the bacterium E. coli. The experiment continues to this day, and is by now probably the largest controlled evolution experiment ever undertaken. Since the inception of the experiment, the bacteria have grown for more than 50,000 generations.
3.2: Graphing Data
3.2.1: Statistical Graphics
Statistical graphics allow results to be displayed in some sort of pictorial form and include scatter plots, histograms, and box plots.
Learning Objective
Recognize the techniques used in exploratory data analysis
Key Points
- Graphical statistical methods explore the content of a data set.
- Graphical statistical methods are used to find structure in data.
- Graphical statistical methods check assumptions in statistical models.
- Graphical statistical methods communicate the results of an analysis.
- Graphical statistical methods communicate the results of an analysis.
Key Terms
- histogram
-
a representation of tabulated frequencies, shown as adjacent rectangles, erected over discrete intervals (bins), with an area equal to the frequency of the observations in the interval
- scatter plot
-
A type of display using Cartesian coordinates to display values for two variables for a set of data.
- box plot
-
A graphical summary of a numerical data sample through five statistics: median, lower quartile, upper quartile, and some indication of more extreme upper and lower values.
Statistical graphics are used to visualize quantitative data. Whereas statistics and data analysis procedures generally yield their output in numeric or tabular form, graphical techniques allow such results to be displayed in some sort of pictorial form. They include plots such as scatter plots , histograms, probability plots, residual plots, box plots, block plots and bi-plots.

An example of a scatter plot
A scatter plot helps identify the type of relationship (if any) between two variables.
Exploratory data analysis (EDA) relies heavily on such techniques. They can also provide insight into a data set to help with testing assumptions, model selection and regression model validation, estimator selection, relationship identification, factor effect determination, and outlier detection. In addition, the choice of appropriate statistical graphics can provide a convincing means of communicating the underlying message that is present in the data to others.
Graphical statistical methods have four objectives:
• The exploration of the content of a data set
• The use to find structure in data
• Checking assumptions in statistical models
• Communicate the results of an analysis.
If one is not using statistical graphics, then one is forfeiting insight into one or more aspects of the underlying structure of the data.
Statistical graphics have been central to the development of science and date to the earliest attempts to analyse data. Many familiar forms, including bivariate plots, statistical maps, bar charts, and coordinate paper were used in the 18th century. Statistical graphics developed through attention to four problems:
• Spatial organization in the 17th and 18th century
• Discrete comparison in the 18th and early 19th century
• Continuous distribution in the 19th century and
• Multivariate distribution and correlation in the late 19th and 20th century.
Since the 1970s statistical graphics have been re-emerging as an important analytic tool with the revitalisation of computer graphics and related technologies.
3.2.2: Stem-and-Leaf Displays
A stem-and-leaf display presents quantitative data in a graphical format to assist in visualizing the shape of a distribution.
Learning Objective
Construct a stem-and-leaf display
Key Points
- Stem-and-leaf displays are useful for displaying the relative density and shape of the data, giving the reader a quick overview of distribution.
- They retain (most of) the raw numerical data, often with perfect integrity. They are also useful for highlighting outliers and finding the mode.
- With very small data sets, a stem-and-leaf displays can be of little use, as a reasonable number of data points are required to establish definitive distribution properties.
- With very large data sets, a stem-and-leaf display will become very cluttered, since each data point must be represented numerically.
Key Terms
- outlier
-
a value in a statistical sample which does not fit a pattern that describes most other data points; specifically, a value that lies 1.5 IQR beyond the upper or lower quartile
- stemplot
-
a means of displaying data used especially in exploratory data analysis; another name for stem-and-leaf display
- histogram
-
a representation of tabulated frequencies, shown as adjacent rectangles, erected over discrete intervals (bins), with an area equal to the frequency of the observations in the interval
A stem-and-leaf display is a device for presenting quantitative data in a graphical format in order to assist in visualizing the shape of a distribution. This graphical technique evolved from Arthur Bowley’s work in the early 1900s, and it is a useful tool in exploratory data analysis. A stem-and-leaf display is often called a stemplot (although, the latter term more specifically refers to another chart type).
Stem-and-leaf displays became more commonly used in the 1980s after the publication of John Tukey ‘s book on exploratory data analysis in 1977. The popularity during those years is attributable to the use of monospaced (typewriter) typestyles that allowed computer technology of the time to easily produce the graphics. However, the superior graphic capabilities of modern computers have lead to the decline of stem-and-leaf displays.
While similar to histograms, stem-and-leaf displays differ in that they retain the original data to at least two significant digits and put the data in order, thereby easing the move to order-based inference and non-parametric statistics.
Construction of Stem-and-Leaf Displays
A basic stem-and-leaf display contains two columns separated by a vertical line. The left column contains the stems and the right column contains the leaves. To construct a stem-and-leaf display, the observations must first be sorted in ascending order. This can be done most easily, if working by hand, by constructing a draft of the stem-and-leaf display with the leaves unsorted, then sorting the leaves to produce the final stem-and-leaf display. Consider the following set of data values:
It must be determined what the stems will represent and what the leaves will represent. Typically, the leaf contains the last digit of the number and the stem contains all of the other digits. In the case of very large numbers, the data values may be rounded to a particular place value (such as the hundreds place) that will be used for the leaves. The remaining digits to the left of the rounded place value are used as the stem. In this example, the leaf represents the ones place and the stem will represent the rest of the number (tens place and higher).
The stem-and-leaf display is drawn with two columns separated by a vertical line. The stems are listed to the left of the vertical line. It is important that each stem is listed only once and that no numbers are skipped, even if it means that some stems have no leaves. The leaves are listed in increasing order in a row to the right of each stem. Note that when there is a repeated number in the data (such as two values of
) then the plot must reflect such. Therefore, the plot would appear as
when it has the numbers
). The display for our data would be as follows:
Now, let’s consider a data set with both negative numbers and numbers that need to be rounded:
For negative numbers, a negative is placed in front of the stem unit, which is still the value
. Non-integers are rounded. This allows the stem-and-leaf plot to retain its shape, even for more complicated data sets:
Applications of Stem-and-Leaf Displays
Stem-and-leaf displays are useful for displaying the relative density and shape of data, giving the reader a quick overview of distribution. They retain (most of) the raw numerical data, often with perfect integrity. They are also useful for highlighting outliers and finding the mode.
However, stem-and-leaf displays are only useful for moderately sized data sets (around 15 to 150 data points). With very small data sets, stem-and-leaf displays can be of little use, as a reasonable number of data points are required to establish definitive distribution properties. With very large data sets, a stem-and-leaf display will become very cluttered, since each data point must be represented numerically. A box plot or histogram may become more appropriate as the data size increases.
Stem-and-Leaf Display
This is an example of a stem-and-leaf display for EPA data on miles per gallon of gasoline.
3.2.3: Reading Points on a Graph
A graph is a representation of a set of objects where some pairs of the objects are connected by links.
Learning Objective
Distinguish direct and indirect edges
Key Points
- The interconnected objects are represented by mathematical abstractions called vertices.
- The links that connect some pairs of vertices are called edges.
- Vertices are also called nodes or points, and edges are also called lines or arcs.
Key Term
- graph
-
A diagram displaying data; in particular one showing the relationship between two or more quantities, measurements or indicative numbers that may or may not have a specific mathematical formula relating them to each other.
In mathematics, a graph is a representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges .Typically, a graph is depicted in diagrammatic form as a set of dots for the vertices, joined by lines or curves for the edges. Graphs are one of the objects of study in discrete mathematics.
The edges may be directed or indirected. For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this is an indirected graph, because if person A shook hands with person B, then person B also shook hands with person A. In contrast, if the vertices represent people at a party, and there is an edge from person A to person B when person A knows of person B, then this graph is directed, because knowledge of someone is not necessarily a symmetric relation (that is, one person knowing another person does not necessarily imply the reverse; for example, many fans may know of a celebrity, but the celebrity is unlikely to know of all their fans). This latter type of graph is called a directed graph and the edges are called directed edges or arcs.Vertices are also called nodes or points, and edges are also called lines or arcs. Graphs are the basic subject studied by graph theory. The word “graph” was first used in this sense by J.J. Sylvester in 1878.
3.2.4: Plotting Points on a Graph
A plot is a graphical technique for representing a data set, usually as a graph showing the relationship between two or more variables.
Learning Objective
Differentiate the different tools used in quantitative and graphical techniques
Key Points
- Graphs are a visual representation of the relationship between variables, very useful because they allow us to quickly derive an understanding which would not come from lists of values.
- Quantitative techniques are the set of statistical procedures that yield numeric or tabular output.
- Examples include hypothesis testing, analysis of variance, point estimates and confidence intervals, and least squares regression.
- There are also many statistical tools generally referred to as graphical techniques, which include: scatter plots, histograms, probability plots, residual plots, box plots, and block plots.
Key Term
- plot
-
a graph or diagram drawn by hand or produced by a mechanical or electronic device
A plot is a graphical technique for representing a data set, usually as a graph showing the relationship between two or more variables. The plot can be drawn by hand or by a mechanical or electronic plotter. Graphs are a visual representation of the relationship between variables, very useful because they allow us to quickly derive an understanding which would not come from lists of values. Graphs can also be used to read off the value of an unknown variable plotted as a function of a known one. Graphs of functions are used in mathematics, sciences, engineering, technology, finance, and many other areas.
Plots play an important role in statistics and data analysis. The procedures here can be broadly split into two parts: quantitative and graphical. Quantitative techniques are the set of statistical procedures that yield numeric or tabular output. Examples of quantitative techniques include:
- hypothesis testing,
- analysis of variance (ANOVA),
- point estimates and confidence intervals, and
- least squares regression.
These and similar techniques are all valuable and are mainstream in terms of classical analysis. There are also many statistical tools generally referred to as graphical techniques. These include:
- scatter plots,
- histograms,
- probability plots,
- residual plots,
- box plots, and
- block plots.
Graphical procedures such as plots are a short path to gaining insight into a data set in terms of testing assumptions, model selection, model validation, estimator selection, relationship identification, factor effect determination, and outlier detection. Statistical graphics give insight into aspects of the underlying structure of the data.
Plotting Points
As an example of plotting points on a graph, consider one of the most important visual aids available to us in the context of statistics: the scatter plot.
To display values for “lung capacity” (first variable) and how long that person could hold his breath, a researcher would choose a group of people to study, then measure each one’s lung capacity (first variable) and how long that person could hold his breath (second variable). The researcher would then plot the data in a scatter plot, assigning “lung capacity” to the horizontal axis, and “time holding breath” to the vertical axis.
A person with a lung capacity of 400 ml who held his breath for 21.7 seconds would be represented by a single dot on the scatter plot at the point
. The scatter plot of all the people in the study would enable the researcher to obtain a visual comparison of the two variables in the data set and will help to determine what kind of relationship there might be between the two variables.
Scatterplot
Scatter plot with a fitted regression line.
3.2.5: Slope and Intercept
The concepts of slope and intercept are essential to understand in the context of graphing data.
Learning Objective
Explain the term rise over run when describing slope
Key Points
- The slope or gradient of a line describes its steepness, incline, or grade — with a higher slope value indicating a steeper incline.
- The slope of a line in the plane containing the
and
axes is generally represented by the letter
, and is defined as the change in the
coordinate divided by the corresponding change in the
coordinate, between two distinct points on the line. - Using the common convention that the horizontal axis represents a variable
and the vertical axis represents a variable
, a
-intercept is a point where the graph of a function or relation intersects with the
-axis of the coordinate system. - Analogously, an
-intercept is a point where the graph of a function or relation intersects with the
-axis.
Key Terms
- intercept
-
the coordinate of the point at which a curve intersects an axis
- slope
-
the ratio of the vertical and horizontal distances between two points on a line; zero if the line is horizontal, undefined if it is vertical.
Slope
The slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline. Slope is normally described by the ratio of the “rise” divided by the “run” between two points on a line. The line may be practical (as for a roadway) or in a diagram.

Slope
The slope of a line in the plane is defined as the rise over the run,
.
The slope of a line in the plane containing the x and y axes is generally represented by the letter m, and is defined as the change in the y coordinate divided by the corresponding change in the x coordinate, between two distinct points on the line. This is described by the following equation:
The Greek letter delta,
, is commonly used in mathematics to mean “difference” or “change”. Given two points
and
, the change in
from one to the other is
(run), while the change in
is
(rise).
Intercept
Using the common convention that the horizontal axis represents a variable
and the vertical axis represents a variable
, a
-intercept is a point where the graph of a function or relation intersects with the
-axis of the coordinate system. It also acts as a reference point for slopes and some graphs.

Intercept
Graph with a
-intercept at
.
If the curve in question is given as
, the
-coordinate of the
-intercept is found by calculating
. Functions which are undefined at
have no
-intercept.
Some 2-dimensional mathematical relationships such as circles, ellipses, and hyperbolas can have more than one
-intercept. Because functions associate
values to no more than one
value as part of their definition, they can have at most one
-intercept.
Analogously, an
-intercept is a point where the graph of a function or relation intersects with the
-axis. As such, these points satisfy
. The zeros, or roots, of such a function or relation are the
-coordinates of these
-intercepts.
3.2.6: Plotting Lines
A line graph is a type of chart which displays information as a series of data points connected by straight line segments.
Learning Objective
Explain the principles of plotting a line graph
Key Points
- A line chart is often used to visualize a trend in data over intervals of time – a time series – thus the line is often drawn chronologically.
- A line chart is typically drawn bordered by two perpendicular lines, called axes. The horizontal axis is called the x-axis and the vertical axis is called the y-axis.
- Typically the y-axis represents the dependent variable and the x-axis (sometimes called the abscissa) represents the independent variable.
- In statistics, charts often include an overlaid mathematical function depicting the best-fit trend of the scattered data.
Key Terms
- bell curve
-
In mathematics, the bell-shaped curve that is typical of the normal distribution.
- line
-
a path through two or more points (compare ‘segment’); a continuous mark, including as made by a pen; any path, curved or straight
- gradient
-
of a function y = f(x) or the graph of such a function, the rate of change of y with respect to x, that is, the amount by which y changes for a certain (often unit) change in x
A line graph is a type of chart which displays information as a series of data points connected by straight line segments. It is a basic type of chart common in many fields. It is similar to a scatter plot except that the measurement points are ordered (typically by their x-axis value) and joined with straight line segments. A line chart is often used to visualize a trend in data over intervals of time – a time series – thus the line is often drawn chronologically.
Plotting
A line chart is typically drawn bordered by two perpendicular lines, called axes. The horizontal axis is called the x-axis and the vertical axis is called the y-axis. To aid visual measurement, there may be additional lines drawn parallel either axis. If lines are drawn parallel to both axes, the resulting lattice is called a grid.
Each axis represents one of the data quantities to be plotted. Typically the y-axis represents the dependent variable and the x-axis (sometimes called the abscissa) represents the independent variable. The chart can then be referred to as a graph of quantity one versus quantity two, plotting quantity one up the y-axis and quantity two along the x-axis.
Example
In the experimental sciences, such as statistics, data collected from experiments are often visualized by a graph. For example, if one were to collect data on the speed of a body at certain points in time, one could visualize the data to look like the graph in :
Data Table
A data table showing elapsed time and measured speed.
The table “visualization” is a great way of displaying exact values, but can be a poor way to understand the underlying patterns that those values represent. Understanding the process described by the data in the table is aided by producing a graph or line chart of Speed versus Time:

Line chart
A graph of speed versus time
Best-Fit
In statistics, charts often include an overlaid mathematical function depicting the best-fit trend of the scattered data. This layer is referred to as a best-fit layer and the graph containing this layer is often referred to as a line graph.
It is simple to construct a “best-fit” layer consisting of a set of line segments connecting adjacent data points; however, such a “best-fit” is usually not an ideal representation of the trend of the underlying scatter data for the following reasons:
1. It is highly improbable that the discontinuities in the slope of the best-fit would correspond exactly with the positions of the measurement values.
2. It is highly unlikely that the experimental error in the data is negligible, yet the curve falls exactly through each of the data points.
In either case, the best-fit layer can reveal trends in the data. Further, measurements such as the gradient or the area under the curve can be made visually, leading to more conclusions or results from the data.
A true best-fit layer should depict a continuous mathematical function whose parameters are determined by using a suitable error-minimization scheme, which appropriately weights the error in the data values. Such curve fitting functionality is often found in graphing software or spreadsheets. Best-fit curves may vary from simple linear equations to more complex quadratic, polynomial, exponential, and periodic curves. The so-called “bell curve”, or normal distribution often used in statistics, is a Gaussian function.
3.2.7: The Equation of a Line
In statistics, linear regression can be used to fit a predictive model to an observed data set of
and
values.
Learning Objective
Examine simple linear regression in terms of slope and intercept
Key Points
- Simple linear regression fits a straight line through a set of points that makes the vertical distances between the points of the data set and the fitted line as small as possible.
-
, where
and
designate constants is a common form of a linear equation. - Linear regression can be used to fit a predictive model to an observed data set of
and
values.
Key Term
- linear regression
-
an approach to modeling the relationship between a scalar dependent variable
$y$ and one or more explanatory variables denoted$x$ .
In statistics, simple linear regression is the least squares estimator of a linear regression model with a single explanatory variable. Simple linear regression fits a straight line through the set of
points in such a way that makes the sum of squared residuals of the model (that is, vertical distances between the points of the data set and the fitted line) as small as possible.
The slope of the fitted line is equal to the correlation between
and
corrected by the ratio of standard deviations of these variables. The intercept of the fitted line is such that it passes through the center of mass
of the data points.

The function of a lne
Three lines — the red and blue lines have the same slope, while the red and green ones have same y-intercept.
Linear regression was the first type of regression analysis to be studied rigorously, and to be used extensively in practical applications. This is because models which depend linearly on their unknown parameters are easier to fit than models which are non-linearly related to their parameters and because the statistical properties of the resulting estimators are easier to determine.
A common form of a linear equation in the two variables
and
is:
Where
(slope) and
(intercept) designate constants. The origin of the name “linear” comes from the fact that the set of solutions of such an equation forms a straight line in the plane. In this particular equation, the constant
determines the slope or gradient of that line, and the constant term
determines the point at which the line crosses the
-axis, otherwise known as the
-intercept.
If the goal is prediction, or forecasting, linear regression can be used to fit a predictive model to an observed data set of
and
values. After developing such a model, if an additional value of
is then given without its accompanying value of
, the fitted model can be used to make a prediction of the value of
.

Linear regression
An example of a simple linear regression analysis
Chapter 2: Statistics in Practice
2.1: Observational Studies
2.1.1: What are Observational Studies?
An observational study is one in which no variables can be manipulated or controlled by the investigator.
Learning Objective
Identify situations in which observational studies are necessary and the challenges that arise in their interpretation.
Key Points
- An observational study is in contrast with experiments, such as randomized controlled trials, where each subject is randomly assigned to a treated group or a control group.
- Variables may be uncontrollable because 1) a randomized experiment would violate ethical standards, 2) the investigator may simply lack the requisite influence, or 3) a randomized experiment may be impractical.
- Observational studies can never identify causal relationships because even though two variables are related both might be caused by a third, unseen, variable.
- A major challenge in conducting observational studies is to draw inferences that are acceptably free from influences by overt biases, as well as to assess the influence of potential hidden biases.
- A major challenge in conducting observational studies is to draw inferences that are acceptably free from influences by overt biases, as well as to assess the influence of potential hidden biases.
Key Terms
- causality
-
the relationship between an event (the cause) and a second event (the effect), where the second event is understood as a consequence of the first
- observational study
-
a study drawing inferences about the possible effect of a treatment on subjects, where the assignment of subjects into a treated group versus a control group is outside the control of the investigator
A common goal in statistical research is to investigate causality, which is the relationship between an event (the cause) and a second event (the effect), where the second event is understood as a consequence of the first. There are two major types of causal statistical studies: experimental studies and observational studies. An observational study draws inferences about the possible effect of a treatment on subjects, where the assignment of subjects into a treated group versus a control group is outside the control of the investigator. This is in contrast with experiments, such as randomized controlled trials, where each subject is randomly assigned to a treated group or a control group. In other words, observational studies have no independent variables — nothing is manipulated by the experimenter. Rather, observations have the equivalent of two dependent variables.
In an observational study, the assignment of treatments may be beyond the control of the investigator for a variety of reasons:
- A randomized experiment would violate ethical standards: Suppose one wanted to investigate the abortion – breast cancer hypothesis, which postulates a causal link between induced abortion and the incidence of breast cancer. In a hypothetical controlled experiment, one would start with a large subject pool of pregnant women and divide them randomly into a treatment group (receiving induced abortions) and a control group (bearing children), and then conduct regular cancer screenings for women from both groups. Needless to say, such an experiment would run counter to common ethical principles. The published studies investigating the abortion–breast cancer hypothesis generally start with a group of women who already have received abortions. Membership in this “treated” group is not controlled by the investigator: the group is formed after the “treatment” has been assigned.
- The investigator may simply lack the requisite influence: Suppose a scientist wants to study the public health effects of a community-wide ban on smoking in public indoor areas. In a controlled experiment, the investigator would randomly pick a set of communities to be in the treatment group. However, it is typically up to each community and/or its legislature to enact a smoking ban. The investigator can be expected to lack the political power to cause precisely those communities in the randomly selected treatment group to pass a smoking ban. In an observational study, the investigator would typically start with a treatment group consisting of those communities where a smoking ban is already in effect.
- A randomized experiment may be impractical: Suppose a researcher wants to study the suspected link between a certain medication and a very rare group of symptoms arising as a side effect. Setting aside any ethical considerations, a randomized experiment would be impractical because of the rarity of the effect. There may not be a subject pool large enough for the symptoms to be observed in at least one treated subject. An observational study would typically start with a group of symptomatic subjects and work backwards to find those who were given the medication and later developed the symptoms
Usefulness and Reliability of Observational Studies
Observational studies can never identify causal relationships because even though two variables are related both might be caused by a third, unseen, variable. Since the underlying laws of nature are assumed to be causal laws, observational findings are generally regarded as less compelling than experimental findings.
Observational studies can, however:
- Provide information on “real world” use and practice
- Detect signals about the benefits and risks of the use of practices in the general population
- Help formulate hypotheses to be tested in subsequent experiments
- Provide part of the community-level data needed to design more informative pragmatic clinical trials
- Inform clinical practice
A major challenge in conducting observational studies is to draw inferences that are acceptably free from influences by overt biases, as well as to assess the influence of potential hidden biases.

Observational Studies
Nature Observation and Study Hall in The Natural and Cultural Gardens, The Expo Memorial Park, Suita city, Osaka, Japan. Observational studies are a type of experiments in which the variables are outside the control of the investigator.
2.1.2: The Clofibrate Trial
The Clofibrate Trial was a placebo-controlled study to determine the safety and effectiveness of drugs treating coronary heart disease in men.
Learning Objective
Outline how the use of placebos in controlled experiments leads to more reliable results.
Key Points
- Clofibrate was one of four lipid-modifying drugs tested in an observational study known as the Coronary Drug Project.
- Placebo-controlled studies are a way of testing a medical therapy in which, in addition to a group of subjects that receives the treatment to be evaluated, a separate control group receives a sham “placebo” treatment which is specifically designed to have no real effect.
- The purpose of the placebo group is to account for the placebo effect — that is, effects from treatment that do not depend on the treatment itself.
- Appropriate use of a placebo in a clinical trial often requires, or at least benefits from, a double-blind study design, which means that neither the experimenters nor the subjects know which subjects are in the “test group” and which are in the “control group. “.
- The use of placebos is a standard control component of most clinical trials which attempt to make some sort of quantitative assessment of the efficacy of medicinal drugs or treatments.
Key Terms
- regression to the mean
-
the phenomenon by which extreme examples from any set of data are likely to be followed by examples which are less extreme; a tendency towards the average of any sample
- placebo
-
an inactive substance or preparation used as a control in an experiment or test to determine the effectiveness of a medicinal drug
- placebo effect
-
the tendency of any medication or treatment, even an inert or ineffective one, to exhibit results simply because the recipient believes that it will work
Clofibrate (tradename Atromid-S) is an organic compound that is marketed as a fibrate. It is a lipid-lowering agent used for controlling the high cholesterol and triacylglyceride level in the blood. Clofibrate was one of four lipid-modifying drugs tested in an observational study known as the Coronary Drug Project. Also known as the World Health Organization Cooperative Trial on Primary Prevention of Ischaemic Heart Disease, the study was a randomized, multi-center, double-blind, placebo-controlled trial that was intended to study the safety and effectiveness of drugs for long-term treatment of coronary heart disease in men.
Placebo-Controlled Observational Studies
Placebo-controlled studies are a way of testing a medical therapy in which, in addition to a group of subjects that receives the treatment to be evaluated, a separate control group receives a sham “placebo” treatment which is specifically designed to have no real effect. Placebos are most commonly used in blinded trials, where subjects do not know whether they are receiving real or placebo treatment.
The purpose of the placebo group is to account for the placebo effect — that is, effects from treatment that do not depend on the treatment itself. Such factors include knowing one is receiving a treatment, attention from health care professionals, and the expectations of a treatment’s effectiveness by those running the research study. Without a placebo group to compare against, it is not possible to know whether the treatment itself had any effect.
Appropriate use of a placebo in a clinical trial often requires, or at least benefits from, a double-blind study design, which means that neither the experimenters nor the subjects know which subjects are in the “test group” and which are in the “control group. ” This creates a problem in creating placebos that can be mistaken for active treatments. Therefore, it can be necessary to use a psychoactive placebo, a drug that produces physiological effects that encourage the belief in the control groups that they have received an active drug.
Patients frequently show improvement even when given a sham or “fake” treatment. Such intentionally inert placebo treatments can take many forms, such as a pill containing only sugar, a surgery where nothing is actually done, or a medical device (such as ultrasound) that is not actually turned on. Also, due to the body’s natural healing ability and statistical effects such as regression to the mean, many patients will get better even when given no treatment at all. Thus, the relevant question when assessing a treatment is not “does the treatment work? ” but “does the treatment work better than a placebo treatment, or no treatment at all? “
Therefore, the use of placebos is a standard control component of most clinical trials which attempt to make some sort of quantitative assessment of the efficacy of medicinal drugs or treatments.
Results of The Coronary Drug Project
Those in the placebo group who adhered to the placebo treatment (took the placebo regularly as instructed) showed nearly half the mortality rate as those who were not adherent. A similar study of women found survival was nearly 2.5 times greater for those who adhered to their placebo. This apparent placebo effect may have occurred because:
- Adhering to the protocol had a psychological effect, i.e. genuine placebo effect.
- People who were already healthier were more able or more inclined to follow the protocol.
- Compliant people were more diligent and health-conscious in all aspects of their lives.
The Coronary Drug Project found that subjects using clofibrate to lower serum cholesterol observed excess mortality in the clofibrate-treated group despite successful cholesterol lowering (47% more deaths during treatment with clofibrate and 5% after treatment with clofibrate) than the non-treated high cholesterol group. These deaths were due to a wide variety of causes other than heart disease, and remain “unexplained”.
Clofibrate was discontinued in 2002 due to adverse affects.
Placebo-Controlled Observational Studies
Prescription placebos used in research and practice.
2.1.3: Confounding
A confounding variable is an extraneous variable in a statistical model that correlates with both the dependent variable and the independent variable.
Learning Objective
Break down why confounding variables may lead to bias and spurious relationships and what can be done to avoid these phenomenons.
Key Points
- A perceived relationship between an independent variable and a dependent variable that has been misestimated due to the failure to account for a confounding factor is termed a spurious relationship.
- Confounding by indication – the most important limitation of observational studies – occurs when prognostic factors cause bias, such as biased estimates of treatment effects in medical trials.
- Confounding variables may also be categorised according to their source: such as operational confounds, procedural confounds or person confounds.
- A reduction in the potential for the occurrence and effect of confounding factors can be obtained by increasing the types and numbers of comparisons performed in an analysis.
- Moreover, depending on the type of study design in place, there are various ways to modify that design to actively exclude or control confounding variables.
Key Terms
- peer review
-
the scholarly process whereby manuscripts intended to be published in an academic journal are reviewed by independent researchers (referees) to evaluate the contribution, i.e. the importance, novelty and accuracy of the manuscript’s contents
- placebo effect
-
the tendency of any medication or treatment, even an inert or ineffective one, to exhibit results simply because the recipient believes that it will work
- prognostic
-
a sign by which a future event may be known or foretold
- confounding variable
-
an extraneous variable in a statistical model that correlates (positively or negatively) with both the dependent variable and the independent variable
Example
- In risk assessments, factors such as age, gender, and educational levels often have impact on health status and so should be controlled. Beyond these factors, researchers may not consider or have access to data on other causal factors. An example is on the study of smoking tobacco on human health. Smoking, drinking alcohol, and diet are lifestyle activities that are related. A risk assessment that looks at the effects of smoking but does not control for alcohol consumption or diet may overestimate the risk of smoking. Smoking and confounding are reviewed in occupational risk assessments such as the safety of coal mining. When there is not a large sample population of non-smokers or non-drinkers in a particular occupation, the risk assessment may be biased towards finding a negative effect on health.
Confounding Variables
A confounding variable is an extraneous variable in a statistical model that correlates (positively or negatively) with both the dependent variable and the independent variable. A perceived relationship between an independent variable and a dependent variable that has been misestimated due to the failure to account for a confounding factor is termed a spurious relationship, and the presence of misestimation for this reason is termed omitted-variable bias.
As an example, suppose that there is a statistical relationship between ice cream consumption and number of drowning deaths for a given period. These two variables have a positive correlation with each other. An individual might attempt to explain this correlation by inferring a causal relationship between the two variables (either that ice cream causes drowning, or that drowning causes ice cream consumption). However, a more likely explanation is that the relationship between ice cream consumption and drowning is spurious and that a third, confounding, variable (the season) influences both variables: during the summer, warmer temperatures lead to increased ice cream consumption as well as more people swimming and, thus, more drowning deaths.
Types of Confounding
Confounding by indication has been described as the most important limitation of observational studies. Confounding by indication occurs when prognostic factors cause bias, such as biased estimates of treatment effects in medical trials. Controlling for known prognostic factors may reduce this problem, but it is always possible that a forgotten or unknown factor was not included or that factors interact complexly. Randomized trials tend to reduce the effects of confounding by indication due to random assignment.
Confounding variables may also be categorised according to their source:
- The choice of measurement instrument (operational confound) – This type of confound occurs when a measure designed to assess a particular construct inadvertently measures something else as well.
- Situational characteristics (procedural confound) – This type of confound occurs when the researcher mistakenly allows another variable to change along with the manipulated independent variable.
- Inter-individual differences (person confound) – This type of confound occurs when two or more groups of units are analyzed together (e.g., workers from different occupations) despite varying according to one or more other (observed or unobserved) characteristics (e.g., gender).
Decreasing the Potential for Confounding
A reduction in the potential for the occurrence and effect of confounding factors can be obtained by increasing the types and numbers of comparisons performed in an analysis. If a relationship holds among different subgroups of analyzed units, confounding may be less likely. That said, if measures or manipulations of core constructs are confounded (i.e., operational or procedural confounds exist), subgroup analysis may not reveal problems in the analysis.
Peer review is a process that can assist in reducing instances of confounding, either before study implementation or after analysis has occurred. Similarly, study replication can test for the robustness of findings from one study under alternative testing conditions or alternative analyses (e.g., controlling for potential confounds not identified in the initial study). Also, confounding effects may be less likely to occur and act similarly at multiple times and locations.
Moreover, depending on the type of study design in place, there are various ways to modify that design to actively exclude or control confounding variables:
- Case-control studies assign confounders to both groups, cases and controls, equally. In case-control studies, matched variables most often are age and sex.
- In cohort studies, a degree of matching is also possible, and it is often done by only admitting certain age groups or a certain sex into the study population. this creates a cohort of people who share similar characteristics; thus, all cohorts are comparable in regard to the possible confounding variable.
- Double blinding conceals the experiment group membership of the participants from the trial population and the observers. By preventing the participants from knowing if they are receiving treatment or not, the placebo effect should be the same for the control and treatment groups. By preventing the observers from knowing of their membership, there should be no bias from researchers treating the groups differently or from interpreting the outcomes differently.
- A randomized controlled trial is a method where the study population is divided randomly in order to mitigate the chances of self-selection by participants or bias by the study designers. Before the experiment begins, the testers will assign the members of the participant pool to their groups (control, intervention, parallel) using a randomization process such as the use of a random number generator.
2.1.4: Sex Bias in Graduate Admissions
The Berkeley study is one of the best known real life examples of an experiment suffering from a confounding variable.
Learning Objective
Illustrate how the phenomenon of confounding can be seen in practice via Simpson’s Paradox.
Key Points
- A study conducted in the aftermath of a law suit filed against the University of California, Berkeley showed that men applying were more likely than women to be admitted.
- Examination of the aggregate data on admissions showed a blatant, if easily misunderstood, pattern of gender discrimination against applicants.
- When examining the individual departments, it appeared that no department was significantly biased against women.
- The study concluded that women tended to apply to competitive departments with low rates of admission even among qualified applicants, whereas men tended to apply to less-competitive departments with high rates of admission among the qualified applicants.
- Simpson’s Paradox is a paradox in which a trend that appears in different groups of data disappears when these groups are combined, and the reverse trend appears for the aggregate data.
Key Terms
- partition
-
a part of something that had been divided, each of its results
- Simpson’s paradox
-
a paradox in which a trend that appears in different groups of data disappears when these groups are combined, and the reverse trend appears for the aggregate data
- aggregate
-
a mass, assemblage, or sum of particulars; something consisting of elements but considered as a whole
Women have traditionally had limited access to higher education. Moreover, when women began to be admitted to higher education, they were encouraged to major in less-intellectual subjects. For example, the study of English literature in American and British colleges and universities was instituted as a field considered suitable to women’s “lesser intellects”.
However, since 1991 the proportion of women enrolled in college in the U.S. has exceeded the enrollment rate for men, and that gap has widened over time. As of 2007, women made up the majority — 54 percent — of the 10.8 million college students enrolled in the U.S.
This has not negated the fact that gender bias exists in higher education. Women tend to score lower on graduate admissions exams, such as the Graduate Record Exam (GRE) and the Graduate Management Admissions Test (GMAT). Representatives of the companies that publish these tests have hypothesized that greater number of female applicants taking these tests pull down women’s average scores. However, statistical research proves this theory wrong. Controlling for the number of people taking the test does not account for the scoring gap.
Sex Bias at the University of California, Berkeley
On February 7, 1975, a study was published in the journal Science by P.J. Bickel, E.A. Hammel, and J.W. O’Connell entitled “Sex Bias in Graduate Admissions: Data from Berkeley. ” This study was conducted in the aftermath of a law suit filed against the University, citing admission figures for the fall of 1973, which showed that men applying were more likely than women to be admitted, and the difference was so large that it was unlikely to be due to chance.
Examination of the aggregate data on admissions showed a blatant, if easily misunderstood, pattern of gender discrimination against applicants.
Aggregate Data:
Men: 8,442 applicants – 44% admitted
Women: 4,321 applicants – 35% admitted
When examining the individual departments, it appeared that no department was significantly biased against women. In fact, most departments had a small but statistically significant bias in favor of women. The data from the six largest departments are listed below.
Department A
Men: 825 applicants – 62% admitted
Women: 108 applicants – 82% admitted
Department B
Men: 560 applicants – 63% admitted
Women: 25 applicants – 68% admitted
Department C
Men: 325 applicants – 37% admitted
Women: 593 applicants – 34% admitted
Department D
Men: 417 applicants – 33% admitted
Women: 375 applicants – 35% admitted
Department E
Men: 191 applicants – 28% admitted
Women: 393 applicants – 24% admitted
Department F
Men: 272 applicants – 6% admitted
Women: 341 applicants – 7% admitted
The research paper by Bickel et al. concluded that women tended to apply to competitive departments with low rates of admission even among qualified applicants (such as in the English Department), whereas men tended to apply to less-competitive departments with high rates of admission among the qualified applicants (such as in engineering and chemistry). The study also concluded that the graduate departments that were easier to enter at the University, at the time, tended to be those that required more undergraduate preparation in mathematics. Therefore, the admission bias seemed to stem from courses previously taken.
Confounding Variables and Simpson’s Paradox
The above study is one of the best known real life examples of an experiment suffering from a confounding variable. In this particular case, we can see an occurrence of Simpson’s Paradox . Simpson’s Paradox is a paradox in which a trend that appears in different groups of data disappears when these groups are combined, and the reverse trend appears for the aggregate data. This result is often encountered in social-science and medical-science statistics, and is particularly confounding when frequency data are unduly given causal interpretations.

Simpson’s Paradox
An illustration of Simpson’s Paradox. For a full explanation of the figure, visit: http://en.wikipedia.org/wiki/Simpson’s_paradox#Description
The practical significance of Simpson’s paradox surfaces in decision making situations where it poses the following dilemma: Which data should we consult in choosing an action, the aggregated or the partitioned? The answer seems to be that one should sometimes follow the partitioned and sometimes the aggregated data, depending on the story behind the data; with each story dictating its own choice.
As to why and how a story, not data, should dictate choices, the answer is that it is the story which encodes the causal relationships among the variables. Once we extract these relationships we can test algorithmically whether a given partition, representing confounding variables, gives the correct answer.

Confounding Variables in Practice
One of the best real life examples of the presence of confounding variables occurred in a study regarding sex bias in graduate admissions here, at the University of California, Berkeley.
2.2: Controlled Experiments
2.2.1: The Salk Vaccine Field Trial
The Salk polio vaccine field trial incorporated a double blind placebo control methodolgy to determine the effectiveness of the vaccine.
Learning Objective
Demonstrate how controls and treatment groups are used in drug testing.
Key Points
- The first effective polio vaccine was developed in 1952 by Jonas Salk at the University of Pittsburgh.
- Roughly 440,000 people received one or more injections of the vaccine, about 210,000 children received a placebo, consisting of harmless culture media, and 1.2 million children received no vaccination and served as a control group, who would then be observed to see if any contracted polio.
- Two serious issues arose in the original experimental design: selection bias and diagnostic bias.
- The combination of randomized control and double-blind experimental factors, which were implemented in the second version of the experimental design, has become the gold standard for a clinical trial.
Key Terms
- control group
-
the group of test subjects left untreated or unexposed to some procedure and then compared with treated subjects in order to validate the results of the test
- placebo
-
an inactive substance or preparation used as a control in an experiment or test to determine the effectiveness of a medicinal drug
The Salk polio vaccine field trials constitute one of the most famous and one of the largest statistical studies ever conducted. The field trials are of particular value to students of statistics because two different experimental designs were used.
Background
The Salk vaccine, or inactivated poliovirus vaccine (IPV), is based on three wild, virulent reference strains:
- Mahoney (type 1 poliovirus),
- MEF-1 (type 2 poliovirus), and
- Saukett (type 3 poliovirus),
grown in a type of monkey kidney tissue culture (Vero cell line), which are then inactivated with formalin. The injected Salk vaccine confers IgG-mediated immunity in the bloodstream, which prevents polio infection from progressing to viremia and protects the motor neurons, thus eliminating the risk of bulbar polio and post-polio syndrome.
The 1954 Field Trial
Statistical tests of new medical treatments almost always have the same basic format. The responses of a treatment group of subjects who are given the treatment are compared to the responses of a control group of subjects who are not given the treatment. The treatment groups and control groups should be as similar as possible.
Beginning February 23, 1954, the vaccine was tested at Arsenal Elementary School and the Watson Home for Children in Pittsburgh, Pennsylvania. Salk’s vaccine was then used in a test called the Francis Field Trial, led by Thomas Francis; the largest medical experiment in history. The test began with some 4,000 children at Franklin Sherman Elementary School in McLean, Virginia, and would eventually involve 1.8 million children, in 44 states from Maine to California. By the conclusion of the study, roughly 440,000 received one or more injections of the vaccine, about 210,000 children received a placebo, consisting of harmless culture media, and 1.2 million children received no vaccination and served as a control group, who would then be observed to see if any contracted polio.
The results of the field trial were announced April 12, 1955 (the 10th anniversary of the death of President Franklin D. Roosevelt, whose paralysis was generally believed to have been caused by polio). The Salk vaccine had been 60–70% effective against PV1 (poliovirus type 1), over 90% effective against PV2 and PV3, and 94% effective against the development of bulbar polio. Soon after Salk’s vaccine was licensed in 1955, children’s vaccination campaigns were launched. In the U.S, following a mass immunization campaign promoted by the March of Dimes, the annual number of polio cases fell from 35,000 in 1953 to 5,600 by 1957. By 1961 only 161 cases were recorded in the United States.
Experimental Design Issues
The original design of the experiment called for second graders (with parental consent) to form the treatment group and first and third graders to form the control group. This design was known as the observed control experiment.
Two serious issues arose in this design: selection bias and diagnostic bias. Because only second graders with permission from their parents were administered the treatment, this treatment group became self-selecting.
Thus, a randomized control design was implemented to overcome these apparent deficiencies. The key distinguishing feature of the randomized control design is that study subjects, after assessment of eligibility and recruitment, but before the intervention to be studied begins, are randomly allocated to receive one or the other of the alternative treatments under study. Therefore, randomized control tends to negate all effects (such as confounding variables) except for the treatment effect.
This design also had the characteristic of being double-blind. Double-blind describes an especially stringent way of conducting an experiment on human test subjects which attempts to eliminate subjective, unrecognized biases carried by an experiment’s subjects and conductors. In a double-blind experiment, neither the participants nor the researchers know which participants belong to the control group, as opposed to the test group. Only after all data have been recorded (and in some cases, analyzed) do the researchers learn which participants were which.
This combination of randomized control and double-blind experimental factors has become the gold standard for a clinical trial.

The Salk Polio Vaccine Field Trial
Jonas Salk administers his polio vaccine on February 26, 1957 in the Commons Room of the Cathedral of Learning at the University of Pittsburgh where the vaccine was created by Salk and his team.
2.2.2: The Portacaval Shunt
Numerous studies have been conducted to examine the value of the portacaval shunt procedure, many using randomized controls.
Learning Objective
Assess the value that the practice of random assignment adds to experimental design.
Key Points
- A portacaval shunt is a treatment for the liver in which a connection is made between the portal vein, which supplies 75% of the liver’s blood, and the inferior vena cava, the vein that drains blood from the lower two-thirds of the body.
- Of the studies on portacaval shunts, 63% were conducted without controls, 29% were conducted with non-randomized controls, and 8% were conducted with randomized controls.
- The thinking behind random assignment is that any effect observed between treatment groups can be linked to the treatment effect and cannot be considered a characteristic of the individuals in the group.
- Because most basic statistical tests require the hypothesis of an independent randomly sampled population, random assignment is the desired assignment method.
Key Terms
- shunt
-
a passage between body channels constructed surgically as a bypass
- random assignment
-
an experimental technique for assigning subjects to different treatments (or no treatment)
A portacaval shunt is a treatment for high blood pressure in the liver. A connection is made between the portal vein, which supplies 75% of the liver’s blood, and the inferior vena cava, the vein that drains blood from the lower two-thirds of the body. The most common causes of liver disease resulting in portal hypertension are cirrhosis , caused by alcohol abuse, and viral hepatitis (hepatitis B and C). Less common causes include diseases such as hemochromatosis, primary biliary cirrhosis (PBC), and portal vein thrombosis. The procedure is long and hazardous .

The Portacaval Shunt
This image is a trichrome stain showing cirrhosis of the liver. Cirrhosis can be combatted by the portacaval shunt procedure, for which there have been numerous experimental trials using randomized assignment.
Numerous studies have been conducted to examine the value of and potential concerns with the surgery. Of these studies, 63% were conducted without controls, 29% were conducted with non-randomized controls, and 8% were conducted with randomized controls.
Randomized Controlled Experiments
Random assignment, or random placement, is an experimental technique for assigning subjects to different treatments (or no treatment). The thinking behind random assignment is that by randomizing treatment assignments, the group attributes for the different treatments will be roughly equivalent; therefore, any effect observed between treatment groups can be linked to the treatment effect and cannot be considered a characteristic of the individuals in the group.
In experimental design, random assignment of participants in experiments or treatment and control groups help to ensure that any differences between and within the groups are not systematic at the outset of the experiment. Random assignment does not guarantee that the groups are “matched” or equivalent, only that any differences are due to chance.
The steps to random assignment include:
- Begin with a collection of subjects – for example, 20 people.
- Devise a method of randomization that is purely mechanical (e.g. flip a coin).
- Assign subjects with “heads” to one group, the control group; assign subjects with “tails” to the other group, the experimental group.
Because most basic statistical tests require the hypothesis of an independent randomly sampled population, random assignment is the desired assignment method. It provides control for all attributes of the members of the samples—in contrast to matching on only one or more variables—and provides the mathematical basis for estimating the likelihood of group equivalence for characteristics one is interested in. This applies both for pre-treatment checks on equivalence and the evaluation of post treatment results using inferential statistics. More advanced statistical modeling can be used to adapt the inference to the sampling method.
2.2.3: Statistical Controls
A scientific control is an observation designed to minimize the effects of variables other than the single independent variable.
Learning Objective
Classify scientific controls and identify how they are used in experiments.
Key Points
- Scientific controls increase the reliability of test results, often through a comparison between control measurements and the other measurements.
- Positive and negative controls, when both are successful, are usually sufficient to eliminate most potential confounding variables.
- Negative controls are groups where no phenomenon is expected. They ensure that there is no effect when there should be no effect.
- Positive controls are groups where a phenomenon is expected. That is, they ensure that there is an effect when there should be an effect.
Key Terms
- confounding variable
-
an extraneous variable in a statistical model that correlates (positively or negatively) with both the dependent variable and the independent variable
- scientific control
-
an experiment or observation designed to minimize the effects of variables other than the single independent variable
What Is a Control?
A scientific control is an observation designed to minimize the effects of variables other than the single independent variable. This increases the reliability of the results, often through a comparison between control measurements and the other measurements.
For example, during drug testing, scientists will try to control two groups to keep them as identical as possible, then allow one group to try the drug. Another example might be testing plant fertilizer by giving it to only half the plants in a garden: the plants that receive no fertilizer are the control group, because they establish the baseline level of growth that the fertilizer-treated plants will be compared against. Without a control group, the experiment cannot determine whether the fertilizer-treated plants grow more than they would have if untreated.
Ideally, all variables in an experiment will be controlled (accounted for by the control measurements) and none will be uncontrolled. In such an experiment, if all the controls work as expected, it is possible to conclude that the experiment is working as intended and that the results of the experiment are due to the effect of the variable being tested. That is, scientific controls allow an investigator to make a claim like “Two situations were identical until factor X occurred. Since factor X is the only difference between the two situations, the new outcome was caused by factor X. “
Controlled Experiments
Controlled experiments can be performed when it is difficult to exactly control all the conditions in an experiment. In this case, the experiment begins by creating two or more sample groups that are probabilistically equivalent, which means that measurements of traits should be similar among the groups and that the groups should respond in the same manner if given the same treatment. This equivalency is determined by statistical methods that take into account the amount of variation between individuals and the number of individuals in each group. In fields such as microbiology and chemistry, where there is very little variation between individuals and the group size is easily in the millions, these statistical methods are often bypassed and simply splitting a solution into equal parts is assumed to produce identical sample groups.
Types of Controls
The simplest types of control are negative and positive controls. These two controls, when both are successful, are usually sufficient to eliminate most potential confounding variables. This means that the experiment produces a negative result when a negative result is expected and a positive result when a positive result is expected.
Negative Controls
Negative controls are groups where no phenomenon is expected. They ensure that there is no effect when there should be no effect. To continue with the example of drug testing, a negative control is a group that has not been administered the drug. We would say that the control group should show a negative or null effect.
If the treatment group and the negative control both produce a negative result, it can be inferred that the treatment had no effect. If the treatment group and the negative control both produce a positive result, it can be inferred that a confounding variable acted on the experiment, and the positive results are likely not due to the treatment.
Positive Controls
Positive controls are groups where a phenomenon is expected. That is, they ensure that there is an effect when there should be an effect. This is accomplished by using an experimental treatment that is already known to produce that effect and then comparing this to the treatment that is being investigated in the experiment.
Positive controls are often used to assess test validity. For example, to assess a new test’s ability to detect a disease, then we can compare it against a different test that is already known to work. The well-established test is the positive control, since we already know that the answer to the question (whether the test works) is yes.
For difficult or complicated experiments, the result from the positive control can also help in comparison to previous experimental results. For example, if the well-established disease test was determined to have the same effectiveness as found by previous experimenters, this indicates that the experiment is being performed in the same way that the previous experimenters did.
When possible, multiple positive controls may be used. For example, if there is more than one disease test that is known to be effective, more than one might be tested. Multiple positive controls also allow finer comparisons of the results (calibration or standardization) if the expected results from the positive controls have different sizes.

Controlled Experiments
An all-female crew of scientific experimenters began a five-day exercise on December 16, 1974. They conducted 11 selected experiments in materials science to determine their practical application for Spacelab missions and to identify integration and operational problems that might occur on actual missions. Air circulation, temperature, humidity and other factors were carefully controlled.
Chapter 1: Introduction to Statistics and Statistical Thinking
1.1: Overview
1.1.1: Collecting and Measuring Data
There are four main levels of measurement: nominal, ordinal, interval, and ratio.
Learning Objective
Distinguish between the nominal, ordinal, interval and ratio methods of data measurement.
Key Points
- Ratio measurements provide the greatest flexibility in statistical methods that can be used for analyzing the data.
- Interval data allows for the degree of difference between items, but not the ratio between them.
- Ordinal measurements have imprecise differences between consecutive values, but have a meaningful order to those values.
- Variables conforming only to nominal or ordinal measurements cannot be reasonably measured numerically, they are often grouped together as categorical variables.
- Ratio and interval measurements are grouped together as quantitative variables.
- Nominal measurements have no meaningful rank order among values.
Key Terms
- sampling
-
the process or technique of obtaining a representative sample
- population
-
a group of units (persons, objects, or other items) enumerated in a census or from which a sample is drawn
Example
- An example of an observational study is one that explores the correlation between smoking and lung cancer. This type of study typically uses a survey to collect observations about the area of interest and then performs statistical analysis. In this case, the researchers would collect observations of both smokers and non-smokers, perhaps through a case-control study, and then look for the number of cases of lung cancer in each group.
There are four main levels of measurement used in statistics: nominal, ordinal, interval, and ratio. Each of these have different degrees of usefulness in statistical research. Data is collected about a population by random sampling .
Nominal measurements have no meaningful rank order among values. Nominal data differentiates between items or subjects based only on qualitative classifications they belong to. Examples include gender, nationality, ethnicity, language, genre, style, biological species, visual pattern, etc.

Defining a population
In applying statistics to a scientific, industrial, or societal problem, it is necessary to begin with a population or process to be studied. Populations can be diverse topics such as “all persons living in a country” or “all stamps produced in the year 1943”.
Ordinal measurements have imprecise differences between consecutive values, but have a meaningful order to those values. Ordinal data allows for rank order (1st, 2nd, 3rd, etc) by which data can be sorted, but it still does not allow for relative degree of difference between them. Examples of ordinal data include dichotomous values such as “sick” versus “healthy” when measuring health, “guilty” versus “innocent” when making judgments in courts, “false” versus “true”, when measuring truth value. Examples also include non-dichotomous data consisting of a spectrum of values, such as “completely agree”, “mostly agree”, “mostly disagree”, or “completely disagree” when measuring opinion.
Interval measurements have meaningful distances between measurements defined, but the zero value is arbitrary (as in the case with longitude and temperature measurements in Celsius or Fahrenheit). Interval data allows for the degree of difference between items, but not the ratio between them. Ratios are not allowed with interval data since 20°C cannot be said to be “twice as hot” as 10°C, nor can multiplication/division be carried out between any two dates directly. However, ratios of differences can be expressed; for example, one difference can be twice another. Interval type variables are sometimes also called “scaled variables”.
Ratio measurements have both a meaningful zero value and the distances between different measurements are defined; they provide the greatest flexibility in statistical methods that can be used for analyzing the data.
Because variables conforming only to nominal or ordinal measurements cannot be reasonably measured numerically, sometimes they are grouped together as categorical variables, whereas ratio and interval measurements are grouped together as quantitative variables, which can be either discrete or continuous, due to their numerical nature.
Measurement processes that generate statistical data are also subject to error. Many of these errors are classified as random (noise) or systematic (bias), but other important types of errors (e.g., blunder, such as when an analyst reports incorrect units) can also be important.
1.1.2: What Is Statistics?
Statistics is the study of the collection, organization, analysis, interpretation, and presentation of data.
Learning Objective
Define the field of Statistics in terms of its definition, application and history.
Key Points
- Statistics combines mathematical and non-mathematical procedures into one discipline.
- Statistics is generally broken down into two categories: descriptive statistics and inferential statistics.
- Statistics is an applied science and is used in many fields, including the natural and social sciences, government, and business.
- The use of statistical methods dates back to at least the 5th century BC.
Key Terms
- statistics
-
a mathematical science concerned with data collection, presentation, analysis, and interpretation
- empirical
-
verifiable by means of scientific experimentation
Example
- Say you want to conduct a poll on whether your school should use its funding to build a new athletic complex or a new library. Appropriate questions to ask would include: How many people do you have to poll? How do you ensure that your poll is free of bias? How do you interpret your results?
Statistics Overview
Statistics is the study of the collection, organization, analysis, interpretation, and presentation of data. It deals with all aspects of data, including the planning of its collection in terms of the design of surveys and experiments. Some consider statistics a mathematical body of science that pertains to the collection, analysis, interpretation or explanation, and presentation of data, while others consider it a branch of mathematics concerned with collecting and interpreting data. Because of its empirical roots and its focus on applications, statistics is usually considered a distinct mathematical science rather than a branch of mathematics. As one would expect, statistics is largely grounded in mathematics, and the study of statistics has lent itself to many major concepts in mathematics, such as:
- probability,
- distributions ,
- samples and populations,
- estimation, and
- data analysis.
However, much of statistics is also non-mathematical. This includes:
- ensuring that data collection is undertaken in a way that produces valid conclusions,
- coding and archiving data so that information is retained and made useful for international comparisons of official statistics,
- reporting of results and summarized data (tables and graphs) in ways comprehensible to those who must use them, and
- implementing procedures that ensure the privacy of census information.
In short, statistics is the study of data. It includes descriptive statistics (the study of methods and tools for collecting data, and mathematical models to describe and interpret data) and inferential statistics (the systems and techniques for making probability-based decisions and accurate predictions based on incomplete data).
How Do We Use Statistics?
A statistician is someone who is particularly well-versed in the ways of thinking necessary to successfully apply statistical analysis. Such people often gain experience through working in any of a wide number of fields. Statisticians improve data quality by developing specific experimental designs and survey samples. Statistics itself also provides tools for predicting and forecasting the use of data and statistical models. Statistics is applicable to a wide variety of academic disciplines, including natural and social sciences, government, and business. Statistical consultants can help organizations and companies that don’t have in-house expertise relevant to their particular questions.
History of Statistics
Statistical methods date back at least to the 5th century BC. The earliest known writing on statistics appears in a 9th century book entitled Manuscript on Deciphering Cryptographic Messages, written by Al-Kindi. In this book, Al-Kindi provides a detailed description of how to use statistics and frequency analysis to decipher encrypted messages. This was the birth of both statistics and cryptanalysis, according to the Saudi engineer Ibrahim Al-Kadi.
The Nuova Cronica, a 14th century history of Florence by the Florentine banker and official Giovanni Villani, includes much statistical information on population, ordinances, commerce, education, and religious facilities, and has been described as the first introduction of statistics as a positive element in history.
Some scholars pinpoint the origin of statistics to 1663, with the publication of Natural and Political Observations upon the Bills of Mortality by John Graunt. Early applications of statistical thinking revolved around the needs of states to base policy on demographic and economic data, hence its “stat-” etymology. The scope of the discipline of statistics broadened in the early 19th century to include the collection and analysis of data in general.
1.1.3: The Purpose of Statistics
Statistics teaches people to use a limited sample to make intelligent and accurate conclusions about a greater population.
Learning Objective
Describe how Statistics helps us to make inferences about a population, understand and interpret variation, and make more informed everyday decisions.
Key Points
- Statistics is an extremely powerful tool available for assessing the significance of experimental data and for drawing the right conclusions from it.
- Statistics helps scientists, engineers, and many other professionals draw the right conclusions from experimental data.
- Variation is ubiquitous in nature, and probability and statistics are the fields that allow us to study, understand, model, embrace and interpret this variation.
Key Terms
- sample
-
a subset of a population selected for measurement, observation, or questioning to provide statistical information about the population
- population
-
a group of units (persons, objects, or other items) enumerated in a census or from which a sample is drawn
Example
- A company selling the cat food brand “Cato” (a fictitious name here), may claim quite truthfully in their advertisements that eight out of ten cat owners said that their cats preferred Cato brand cat food to “the other leading brand” cat food. What they may not mention is that the cat owners questioned were those they found in a supermarket buying Cato, which doesn’t represent an unbiased sample of cat owners.
Imagine reading a book for the first few chapters and then being able to get a sense of what the ending will be like. This ability is provided by the field of inferential statistics. With the appropriate tools and solid grounding in the field, one can use a limited sample (e.g., reading the first five chapters of Pride & Prejudice) to make intelligent and accurate statements about the population (e.g., predicting the ending of Pride & Prejudice).
Those proceeding to higher education will learn that statistics is an extremely powerful tool available for assessing the significance of experimental data and for drawing the right conclusions from the vast amounts of data encountered by engineers, scientists, sociologists, and other professionals in most spheres of learning. There is no study with scientific, clinical, social, health, environmental or political goals that does not rely on statistical methodologies. The most essential reason for this fact is that variation is ubiquitous in nature, and probability and statistics are the fields that allow us to study, understand, model, embrace and interpret this variation.
In today’s information-overloaded age, statistics is one of the most useful subjects anyone can learn. Newspapers are filled with statistical data, and anyone who is ignorant of statistics is at risk of being seriously misled about important real-life decisions such as what to eat, who is leading the polls, how dangerous smoking is, et cetera. Statistics are often used by politicians, advertisers, and others to twist the truth for their own gain. Knowing at least a little about the field of statistics will help one to make more informed decisions about these and other important questions.

The Purpose of Statistics
Statistics teaches people to use a limited sample to make intelligent and accurate conclusions about a greater population. The use of tables, graphs, and charts play a vital role in presenting the data being used to draw these conclusions.
1.1.4: Inferential Statistics
The mathematical procedure in which we make intelligent guesses about a population based on a sample is called inferential statistics.
Learning Objective
Discuss how inferential statistics allows us to draw conclusions about a population from a random sample and corresponding tests of significance.
Key Points
- Inferential statistics is used to describe systems of procedures that can be used to draw conclusions from data sets arising from systems affected by random variation, such as observational errors, random sampling, or random experimentation.
- Samples must be representative of the entire population in order to induce a conclusion about that population.
- Statisticians use tests of significance to determine the probability that the results were found by chance.
Key Term
- inferential statistics
-
A branch of mathematics that involves drawing conclusions about a population based on sample data drawn from it.
In statistics, statistical inference is the process of drawing conclusions from data that is subject to random variation–for example, observational errors or sampling variation. More substantially, the terms statistical inference, statistical induction, and inferential statistics are used to describe systems of procedures that can be used to draw conclusions from data sets arising from systems affected by random variation, such as observational errors, random sampling, or random experimentation. Initial requirements of such a system of procedures for inference and induction are that the system should produce reasonable answers when applied to well-defined situations and that it should be general enough to be applied across a range of situations.
The outcome of statistical inference may be an answer to the question “what should be done next? ” where this might be a decision about making further experiments or surveys, or about drawing a conclusion before implementing some organizational or governmental policy.
Suppose you have been hired by the National Election Commission to examine how the American people feel about the fairness of the voting procedures in the U.S. How will you do it? Who will you ask?
It is not practical to ask every single American how he or she feels about the fairness of the voting procedures. Instead, we query a relatively small number of Americans, and draw inferences about the entire country from their responses. The Americans actually queried constitute our sample of the larger population of all Americans. The mathematical procedures whereby we convert information about the sample into intelligent guesses about the population fall under the rubric of inferential statistics.
In the case of voting attitudes, we would sample a few thousand Americans, drawn from the hundreds of millions that make up the country. In choosing a sample, it is therefore crucial that it be representative. It must not over-represent one kind of citizen at the expense of others. For example, something would be wrong with our sample if it happened to be made up entirely of Florida residents. If the sample held only Floridians, it could not be used to infer the attitudes of other Americans. The same problem would arise if the sample were comprised only of Republicans. Inferential statistics are based on the assumption that sampling is random. We trust a random sample to represent different segments of society in close to the appropriate proportions (provided the sample is large enough).
Furthermore, when generalizing a trend found in a sample to the larger population, statisticians uses tests of significance (such as the Chi-Square test or the T-test). These tests determine the probability that the results found were by chance, and therefore not representative of the entire population.

Linear Regression in Inferential Statistics
This graph shows a linear regression model, which is a tool used to make inferences in statistics.
1.1.5: Types of Data
Data can be categorized as either primary or secondary and as either qualitative or quantitative.
Learning Objective
Differentiate between primary and secondary data and qualitative and quantitative data.
Key Points
- Primary data is data collected first-hand. Secondary data is data reused from another source.
- Qualitative data is a categorical measurement expressed not in terms of numbers, but rather by means of a natural language description.
- Quantitative data is a numerical measurement expressed not by means of a natural language description, but rather in terms of numbers.
Key Terms
- primary data
-
data that has been compiled for a specific purpose, and has not been collated or merged with others
- qualitative data
-
data centered around descriptions or distinctions based on some quality or characteristic rather than on some quantity or measured value
- quantitative
-
of a measurement based on some quantity or number rather than on some quality
Example
- Qualitative data: race, religion, gender, etc. Quantitative data: height in inches, time in seconds, temperature in degrees, etc.
Primary and Secondary Data
Data can be classified as either primary or secondary. Primary data is original data that has been collected specially for the purpose in mind. This type of data is collected first hand. Those who gather primary data may be an authorized organization, investigator, enumerator or just someone with a clipboard. These people are acting as a witness, so primary data is only considered as reliable as the people who gather it. Research where one gathers this kind of data is referred to as field research. An example of primary data is conducting your own questionnaire.
Secondary data is data that has been collected for another purpose. This type of data is reused, usually in a different context from its first use. You are not the original source of the data–rather, you are collecting it from elsewhere. An example of secondary data is using numbers and information found inside a textbook.
Knowing how the data was collected allows critics of a study to search for bias in how it was conducted. A good study will welcome such scrutiny. Each type has its own weaknesses and strengths. Primary data is gathered by people who can focus directly on the purpose in mind. This helps ensure that questions are meaningful to the purpose, but this can introduce bias in those same questions. Secondary data doesn’t have the privilege of this focus, but is only susceptible to bias introduced in the choice of what data to reuse. Stated another way, those who gather secondary data get to pick the questions. Those who gather primary data get to write the questions. There may be bias either way.
Qualitative and Quantitative Data
Qualitative data is a categorical measurement expressed not in terms of numbers, but rather by means of a natural language description. In statistics, it is often used interchangeably with “categorical” data. Collecting information about a favorite color is an example of collecting qualitative data. Although we may have categories, the categories may have a structure to them. When there is not a natural ordering of the categories, we call these nominal categories. Examples might be gender, race, religion, or sport. When the categories may be ordered, these are called ordinal categories. Categorical data that judge size (small, medium, large, etc. ) are ordinal categories. Attitudes (strongly disagree, disagree, neutral, agree, strongly agree) are also ordinal categories; however, we may not know which value is the best or worst of these issues. Note that the distance between these categories is not something we can measure.
Quantitative data is a numerical measurement expressed not by means of a natural language description, but rather in terms of numbers. Quantitative data always are associated with a scale measure. Probably the most common scale type is the ratio-scale. Observations of this type are on a scale that has a meaningful zero value but also have an equidistant measure (i.e. the difference between 10 and 20 is the same as the difference between 100 and 110). For example, a 10 year-old girl is twice as old as a 5 year-old girl. Since you can measure zero years, time is a ratio-scale variable. Money is another common ratio-scale quantitative measure. Observations that you count are usually ratio-scale (e.g. number of widgets). A more general quantitative measure is the interval scale. Interval scales also have an equidistant measure. However, the doubling principle breaks down in this scale. A temperature of 50 degrees Celsius is not “half as hot” as a temperature of 100, but a difference of 10 degrees indicates the same difference in temperature anywhere along the scale.

Quantitative Data
The graph shows a display of quantitative data.
1.1.6: Applications of Statistics
Statistics deals with all aspects of the collection, organization, analysis, interpretation, and presentation of data.
Learning Objective
Describe how statistics is applied to scientific, industrial, and societal problems.
Key Points
- Statistics can be used to improve data quality by developing specific experimental designs and survey samples.
- Statistics includes the planning of data collection in terms of the design of surveys and experiments.
- Statistics provides tools for prediction and forecasting and is applicable to a wide variety of academic disciplines, including natural and social sciences, as well as government, and business.
Key Terms
- population
-
a group of units (persons, objects, or other items) enumerated in a census or from which a sample is drawn
- statistics
-
The study of the collection, organization, analysis, interpretation, and presentation of data.
- sample
-
a subset of a population selected for measurement, observation, or questioning to provide statistical information about the population
Example
- In calculating the arithmetic mean of a sample, for example, the algorithm works by summing all the data values observed in the sample and then dividing this sum by the number of data items. This single measure, the mean of the sample, is called a statistic; its value is frequently used as an estimate of the mean value of all items comprising the population from which the sample is drawn. The population mean is also a single measure; however, it is not called a statistic; instead it is called a population parameter.
Statistics deals with all aspects of the collection, organization, analysis, interpretation, and presentation of data. It includes the planning of data collection in terms of the design of surveys and experiments.
Statistics can be used to improve data quality by developing specific experimental designs and survey samples. Statistics also provides tools for prediction and forecasting. Statistics is applicable to a wide variety of academic disciplines, including natural and social sciences as well as government and business. Statistical consultants can help organizations and companies that don’t have in-house expertise relevant to their particular questions.
Descriptive and Inferential Statistics
Statistical methods can summarize or describe a collection of data. This is called descriptive statistics . This is particularly useful in communicating the results of experiments and research. Statistical models can also be used to draw statistical inferences about the process or population under study—a practice called inferential statistics. Inference is a vital element of scientific advancement, since it provides a way to draw conclusions from data that are subject to random variation. Conclusions are tested in order to prove the propositions being investigated further, as part of the scientific method. Descriptive statistics and analysis of the new data tend to provide more information as to the truth of the proposition.

Summary statistics
In descriptive statistics, summary statistics are used to summarize a set of observations, in order to communicate the largest amount as simply as possible. This Boxplot represents Michelson and Morley’s data on the speed of light. It consists of five experiments, each made of 20 consecutive runs.
The Statistical Process
When applying statistics to a scientific, industrial, or societal problems, it is necessary to begin with a population or process to be studied. Populations can be diverse topics such as “all persons living in a country” or “every atom composing a crystal”. A population can also be composed of observations of a process at various times, with the data from each observation serving as a different member of the overall group. Data collected about this kind of “population” constitutes what is called a time series. For practical reasons, a chosen subset of the population called a sample is studied—as opposed to compiling data about the entire group (an operation called census). Once a sample that is representative of the population is determined, data is collected for the sample members in an observational or experimental setting. This data can then be subjected to statistical analysis, serving two related purposes: description and inference.
Descriptive statistics summarize the population data by describing what was observed in the sample numerically or graphically. Numerical descriptors include mean and standard deviation for continuous data types (like heights or weights), while frequency and percentage are more useful in terms of describing categorical data (like race). Inferential statistics uses patterns in the sample data to draw inferences about the population represented, accounting for randomness. These inferences may take the form of: answering yes/no questions about the data (hypothesis testing), estimating numerical characteristics of the data (estimation), describing associations within the data (correlation) and modeling relationships within the data (for example, using regression analysis). Inference can extend to forecasting, prediction and estimation of unobserved values either in or associated with the population being studied. It can include extrapolation and interpolation of time series or spatial data and can also include data mining.
Statistical Analysis
Statistical analysis of a data set often reveals that two variables of the population under consideration tend to vary together, as if they were connected. For example, a study of annual income that also looks at age of death might find that poor people tend to have shorter lives than affluent people. The two variables are said to be correlated; however, they may or may not be the cause of one another. The correlation could be caused by a third, previously unconsidered phenomenon, called a confounding variable. For this reason, there is no way to immediately infer the existence of a causal relationship between the two variables.
To use a sample as a guide to an entire population, it is important that it truly represent the overall population. Representative sampling assures that inferences and conclusions can safely extend from the sample to the population as a whole. A major problem lies in determining the extent that the sample chosen is actually representative. Statistics offers methods to estimate and correct for any random trending within the sample and data collection procedures. There are also methods of experimental design for experiments that can lessen these issues at the outset of a study, strengthening its capability to discern truths about the population. Randomness is studied using the mathematical discipline of probability theory. Probability is used in “mathematical statistics” (alternatively, “statistical theory”) to study the sampling distributions of sample statistics and, more generally, the properties of statistical procedures. The use of any statistical method is valid when the system or population under consideration satisfies the assumptions of the method.
1.1.7: Fundamentals of Statistics
In applying statistics to a scientific, industrial, or societal problem, it is necessary to begin with a population or process to be studied.
Learning Objective
Recall that the field of Statistics involves using samples to make inferences about populations and describing how variables relate to each other.
Key Points
- For practical reasons, a chosen subset of the population called a sample is studied—as opposed to compiling data about the entire group (an operation called census).
- Descriptive statistics summarizes the population data by describing what was observed in the sample numerically or graphically.
- Inferential statistics uses patterns in the sample data to draw inferences about the population represented, accounting for randomness.
- Statistical analysis of a data set often reveals that two variables (properties) of the population under consideration tend to vary together, as if they were connected.
- To use a sample as a guide to an entire population, it is important that it truly represent the overall population.
Key Terms
- sample
-
a subset of a population selected for measurement, observation, or questioning to provide statistical information about the population
- variable
-
a quantity that may assume any one of a set of values
- population
-
a group of units (persons, objects, or other items) enumerated in a census or from which a sample is drawn
Example
- A population can be composed of observations of a process at various times, with the data from each observation serving as a different member of the overall group. Data collected about this kind of “population” constitutes what is called a time series.
In applying statistics to a scientific, industrial, or societal problem, it is necessary to begin with a population or process to be studied. Populations can be diverse topics such as “all persons living in a country” or “every atom composing a crystal.”. A population can also be composed of observations of a process at various times, with the data from each observation serving as a different member of the overall group. Data collected about this kind of “population” constitutes what is called a time series.
For practical reasons, a chosen subset of the population called a sample is studied—as opposed to compiling data about the entire group (an operation called census). Once a sample that is representative of the population is determined, data is collected for the sample members in an observational or experimental setting. This data can then be subjected to statistical analysis, serving two related purposes: description and inference.
- Descriptive statistics summarizes the population data by describing what was observed in the sample numerically or graphically. Numerical descriptors include mean and standard deviation for continuous data types (like heights or weights), while frequency and percentages are more useful in terms of describing categorical data (like race).
- Inferential statistics uses patterns in the sample data to draw inferences about the population represented, accounting for randomness. These inferences may take the form of: answering yes/no questions about the data (hypothesis testing), estimating numerical characteristics of the data (estimation), describing associations within the data (correlation ) and modeling relationships within the data (for example, using regression analysis). Inference can extend to forecasting, prediction and estimation of unobserved values either in or associated with the population being studied. It can include extrapolation and interpolation of time series or spatial data, and can also include data mining.
The concept of correlation is particularly noteworthy for the potential confusion it can cause. Statistical analysis of a data set often reveals that two variables (properties) of the population under consideration tend to vary together, as if they were connected. For example, a study of annual income that also looks at age of death might find that poor people tend to have shorter lives than affluent people. The two variables are said to be correlated; however, they may or may not be the cause of one another. The correlation phenomena could be caused by a third, previously unconsidered phenomenon, called a confounding variable. For this reason, there is no way to immediately infer the existence of a causal relationship between the two variables.
To use a sample as a guide to an entire population, it is important that it truly represent the overall population. Representative sampling assures that inferences and conclusions can safely extend from the sample to the population as a whole. A major problem lies in determining the extent that the sample chosen is actually representative. Statistics offers methods to estimate and correct for any random trending within the sample and data collection procedures. There are also methods of experimental design for experiments that can lessen these issues at the outset of a study, strengthening its capability to discern truths about the population.
Randomness is studied using the mathematical discipline of probability theory. Probability is used in “mathematical statistics” (alternatively, “statistical theory”) to study the sampling distributions of sample statistics and, more generally, the properties of statistical procedures. The use of any statistical method is valid when the system or population under consideration satisfies the assumptions of the method.
1.1.8: Critical Thinking
The essential skill of critical thinking will go a long way in helping one to develop statistical literacy.
Learning Objective
Interpret the role that the process of critical thinking plays in statistical literacy.
Key Points
- Statistics can be made to produce misrepresentations of data that may seem valid.
- Statistical literacy is necessary to understand what makes a poll trustworthy and to properly weigh the value of poll results and conclusions.
- Critical thinking is a way of deciding whether a claim is always true, sometimes true, partly true, or false.
- The list of core critical thinking skills includes observation, interpretation, analysis, inference, evaluation, explanation, and meta-cognition.
Key Terms
- statistical literacy
-
the ability to understand statistics, necessary for citizens to understand mateiral presented in publications such as newspapers, television, and the Internet
- critical thinking
-
the application of logical principles, rigorous standards of evidence, and careful reasoning to the analysis and discussion of claims, beliefs, and issues
Each day people are inundated with statistical information from advertisements (“4 out of 5 dentists recommend”), news reports (“opinion polls show the incumbent leading by four points”), and even general conversation (“half the time I don’t know what you’re talking about”). Experts and advocates often use numerical claims to bolster their arguments, and statistical literacy is a necessary skill to help one decide what experts mean and which advocates to believe. This is important because statistics can be made to produce misrepresentations of data that may seem valid. The aim of statistical literacy is to improve the public understanding of numbers and figures.
For example, results of opinion polling are often cited by news organizations, but the quality of such polls varies considerably. Some understanding of the statistical technique of sampling is necessary in order to be able to correctly interpret polling results. Sample sizes may be too small to draw meaningful conclusions, and samples may be biased. The wording of a poll question may introduce a bias, and thus can even be used intentionally to produce a biased result. Good polls use unbiased techniques, with much time and effort being spent in the design of the questions and polling strategy. Statistical literacy is necessary to understand what makes a poll trustworthy and to properly weigh the value of poll results and conclusions.
Critical Thinking
The essential skill of critical thinking will go a long way in helping one to develop statistical literacy. Critical thinking is a way of deciding whether a claim is always true, sometimes true, partly true, or false. The list of core critical thinking skills includes observation, interpretation, analysis, inference, evaluation, explanation, and meta-cognition. There is a reasonable level of consensus that an individual or group engaged in strong critical thinking gives due consideration to establish:
- Evidence through observation,
- Context skills,
- Relevant criteria for making the judgment well,
- Applicable methods or techniques for forming the judgment, and
- Applicable theoretical constructs for understanding the problem and the question at hand.
Critical thinking calls for the ability to:
- Recognize problems, to find workable means for meeting those problems,
- Understand the importance of prioritization and order of precedence in problem solving,
- Gather and marshal pertinent (relevant) information,
- Recognize unstated assumptions and values,
- Comprehend and use language with accuracy, clarity, and discernment,
- Interpret data, to appraise evidence and evaluate arguments,
- Recognize the existence (or non-existence) of logical relationships between propositions,
- Draw warranted conclusions and generalizations,
- Put to test the conclusions and generalizations at which one arrives,
- Reconstruct one’s patterns of beliefs on the basis of wider experience, and
- Render accurate judgments about specific things and qualities in everyday life.
Critical Thinking
Critical thinking is an inherent part of data analysis and statistical literacy.
1.1.9: Experimental Design
Experimental design is the design of studies where variation, which may or may not be under full control of the experimenter, is present.
Learning Objective
Outline the methodology for designing experiments in terms of comparison, randomization, replication, blocking, orthogonality, and factorial experiments
Key Points
- The experimenter is often interested in the effect of some process or intervention (the “treatment”) on some objects (the “experimental units”), which may be people, parts of people, groups of people, plants, animals, etc.
- A methodology for designing experiments involves comparison, randomization, replication, blocking, orthogonality, and factorial considerations.
- It is best that a process be in reasonable statistical control prior to conducting designed experiments.
- One of the most important requirements of experimental research designs is the necessity of eliminating the effects of spurious, intervening, and antecedent variables.
Key Terms
- dependent variable
-
in an equation, the variable whose value depends on one or more variables in the equation
- independent variable
-
in an equation, any variable whose value is not dependent on any other in the equation
- experiment
-
A test under controlled conditions made to either demonstrate a known truth, examine the validity of a hypothesis, or determine the efficacy of something previously untried.
Example
- For example, if a researcher feeds an experimental artificial sweetener to sixty laboratory rats and observes that ten of them subsequently become sick, the underlying cause could be the sweetener itself or something unrelated. Other variables, which may not be readily obvious, may interfere with the experimental design. For instance, perhaps the rats were simply not supplied with enough food or water, or the water was contaminated and undrinkable, or the rats were under some psychological or physiological stress, etc. Eliminating each of these possible explanations individually would be time-consuming and difficult. However, if a control group is used that does not receive the sweetener but is otherwise treated identically, any difference between the two groups can be ascribed to the sweetener itself with much greater confidence.
In general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. Formal planned experimentation is often used in evaluating physical objects, chemical formulations, structures, components, and materials. In the design of experiments, the experimenter is often interested in the effect of some process or intervention (the “treatment”) on some objects (the “experimental units”), which may be people, parts of people, groups of people, plants, animals, etc. Design of experiments is thus a discipline that has very broad application across all the natural and social sciences and engineering.
A methodology for designing experiments was proposed by Ronald A. Fisher in his innovative books The Arrangement of Field Experiments (1926) and The Design of Experiments (1935). These methods have been broadly adapted in the physical and social sciences.

Old-fashioned scale
A scale is emblematic of the methodology of experimental design which includes comparison, replication, and factorial considerations.
- Comparison: In some fields of study it is not possible to have independent measurements to a traceable standard. Comparisons between treatments are much more valuable and are usually preferable. Often one compares against a scientific control or traditional treatment that acts as baseline.
- Randomization: Random assignment is the process of assigning individuals at random to groups or to different groups in an experiment. The random assignment of individuals to groups (or conditions within a group) distinguishes a rigorous, “true” experiment from an adequate, but less-than-rigorous, “quasi-experiment”. Random does not mean haphazard, and great care must be taken that appropriate random methods are used.
- Replication: Measurements are usually subject to variation and uncertainty. Measurements are repeated and full experiments are replicated to help identify the sources of variation, to better estimate the true effects of treatments, to further strengthen the experiment’s reliability and validity, and to add to the existing knowledge of the topic.
- Blocking: Blocking is the arrangement of experimental units into groups (blocks) consisting of units that are similar to one another. Blocking reduces known but irrelevant sources of variation between units and thus allows greater precision in the estimation of the source of variation under study.
- Orthogonality: Orthogonality concerns the forms of comparison (contrasts) that can be legitimately and efficiently carried out. Contrasts can be represented by vectors and sets of orthogonal contrasts are uncorrelated and independently distributed if the data are normal. Because of this independence, each orthogonal treatment provides different information to the others. If there are
treatments and
orthogonal contrasts, all the information that can be captured from the experiment is obtainable from the set of contrasts. - Factorial experiments: Use of factorial experiments instead of the one-factor-at-a-time method. These are efficient at evaluating the effects and possible interactions of several factors (independent variables). Analysis of experiment design is built on the foundation of the analysis of variance, a collection of models that partition the observed variance into components, according to what factors the experiment must estimate or test.
It is best that a process be in reasonable statistical control prior to conducting designed experiments. When this is not possible, proper blocking, replication, and randomization allow for the careful conduct of designed experiments. To control for nuisance variables, researchers institute control checks as additional measures. Investigators should ensure that uncontrolled influences (e.g., source credibility perception) are measured do not skew the findings of the study.
One of the most important requirements of experimental research designs is the necessity of eliminating the effects of spurious, intervening, and antecedent variables. In the most basic model, cause (
) leads to effect (
). But there could be a third variable (
) that influences (
), and
might not be the true cause at all.
is said to be a spurious variable and must be controlled for. The same is true for intervening variables (a variable in between the supposed cause (
) and the effect (
)), and anteceding variables (a variable prior to the supposed cause (
) that is the true cause). In most designs, only one of these causes is manipulated at a time.
1.1.10: Random Samples
An unbiased random selection of individuals is important so that in the long run, the sample represents the population.
Learning Objective
Explain how simple random sampling leads to every object having the same possibility of being chosen.
Key Points
- Simple random sampling merely allows one to draw externally valid conclusions about the entire population based on the sample.
- Advantages of random sampling are that it is free of classification error, and it requires minimum advance knowledge of the population other than the frame.
- Simple random sampling best suits situations where not much information is available about the population and data collection can be efficiently conducted on randomly distributed items, or where the cost of sampling is small enough to make efficiency less important than simplicity.
Key Terms
- population
-
a group of units (persons, objects, or other items) enumerated in a census or from which a sample is drawn
- random sample
-
a sample randomly taken from an investigated population
Sampling is concerned with the selection of a subset of individuals from within a statistical population to estimate characteristics of the whole population . Two advantages of sampling are that the cost is lower and data collection is faster than measuring the entire population.
Random Sampling
MIME types of a random sample of supplementary materials from the Open Access subset in PubMed Central as of October 23, 2012. The colour code means that the MIME type of the supplementary files is indicated correctly (green) or incorrectly (red) in the XML at PubMed Central.
Each observation measures one or more properties (such as weight, location, color) of observable bodies distinguished as independent objects or individuals. In survey sampling, weights can be applied to the data to adjust for the sample design, particularly stratified sampling (blocking). Results from probability theory and statistical theory are employed to guide practice. In business and medical research, sampling is widely used for gathering information about a population.
A simple random sample is a subset of individuals chosen from a larger set (a population). Each individual is chosen randomly and entirely by chance, such that each individual has the same probability of being chosen at any stage during the sampling process and each subset of
individuals has the same probability of being chosen for the sample as any other subset of
individuals. A simple random sample is an unbiased surveying technique.
Simple random sampling is a basic type of sampling, since it can be a component of other more complex sampling methods. The principle of simple random sampling is that every object has the same possibility to be chosen. For example,
college students want to get a ticket for a basketball game, but there are not enough tickets (
) for them, so they decide to have a fair way to see who gets to go. Then, everybody is given a number (0 to
), and random numbers are generated. The first
numbers would be the lucky ticket winners.
In small populations and often in large ones, such sampling is typically done “without replacement” (i.e., one deliberately avoids choosing any member of the population more than once). Although simple random sampling can be conducted with replacement instead, this is less common and would normally be described more fully as simple random sampling with replacement. Sampling done without replacement is no longer independent, but still satisfies exchangeability. Hence, many results still hold. Further, for a small sample from a large population, sampling without replacement is approximately the same as sampling with replacement, since the odds of choosing the same individual twice is low.
An unbiased random selection of individuals is important so that, in the long run, the sample represents the population. However, this does not guarantee that a particular sample is a perfect representation of the population. Simple random sampling merely allows one to draw externally valid conclusions about the entire population based on the sample.
Conceptually, simple random sampling is the simplest of the probability sampling techniques. It requires a complete sampling frame, which may not be available or feasible to construct for large populations. Even if a complete frame is available, more efficient approaches may be possible if other useful information is available about the units in the population.
Advantages are that it is free of classification error, and it requires minimum advance knowledge of the population other than the frame. Its simplicity also makes it relatively easy to interpret data collected via SRS. For these reasons, simple random sampling best suits situations where not much information is available about the population and data collection can be efficiently conducted on randomly distributed items, or where the cost of sampling is small enough to make efficiency less important than simplicity. If these conditions are not true, stratified sampling or cluster sampling may be a better choice.
